任何流动问题都必须满足质量守恒定律。为了避免方程形式对坐标系的依赖，我们首先来推导积分形式的守恒方程，然后得到其微分形式。

基于不同的描述方法，质量守恒定律有不同的表示。在拉格朗日描述下，如图2.5 所示，由于作为研究对象的流体团是封闭系统，质量守恒表述为流体团质量不变，假设该流体团此时刚好与某一控制体重合，则有

其中，ρ 为流体密度。

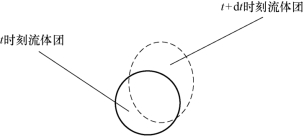
图2.5　同一团流体不同时刻质量不变

而在欧拉描述下，如图2.6 所示，质量守恒表示为单位时间控制体内流体质量的增加量，等于流入控制体内的流体质量，即

其中，V 为流体速度矢量；dS 为控制体表面的微元面积矢量，方向垂直于表面向外。由于控制体不随时间变化，因此可以将式（2.9）左端的求导运算放入积分中，同时对式（2.9）右端应用高斯定理，可以得到

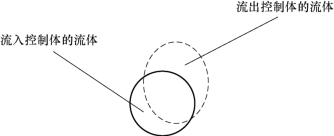
图2.6　控制体流入流出

式（2.11）即欧拉描述下积分形式的质量守恒方程。

下面来推导微分形式的质量守恒方程。首先推导拉格朗日描述下的微分形式。对于式（2.8），由于流体团的体积随时间变化，因此无法直接将方程左边对时间的求导运算与积分运算交换次序。为了便于理解，我们首先取流体微团（而不是流体团）作为研究对象，可以得到(www.daowen.com)

其中，δΩ 为流体微团的体积。将式（2.12）展开后整理可得

根据散度的数学定义，我们可以得到

接下来推导欧拉描述下的微分形式。由于式（2.11）对任意控制体成立，因此，对于微元控制体也必然成立，由此可得欧拉描述下质量守恒方程的微分形式

至此，两种描述下的微分形式的质量守恒方程都已得到。然而，虽然我们可以用同样的方法得到动量守恒方程与能量守恒方程，但是它们在形式上不够简化直观。为此，我们需要在后面的推导中利用质量守恒方程对其进行简化。将式（2.14）与式（2.15）结合并确保量纲一致可得

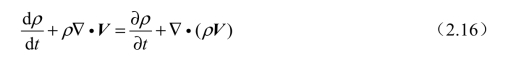
由于nabla 算子本质上仍然是求导运算，因此可以运用求导的乘法法则：

最后将式（2.17）代入式（2.16）并整理后可得

式（2.18）具有十分重要的意义，它构建了流体微团与控制体密度变化率之间的关系。实际上，将参数ρ 直接代入式（2.7）中的参数φ 可以得到相同的关系式。这里用不同的方法推导，有助于加深读者对于两种描述方法的理解。