世间的流体运动千姿百态，变化多端。要定量地研究气体运动的规律，首先要对气体运动进行描述。对于气体运动的描述，主要有两种方法。一种是拉格朗日描述。是的，这是一位和牛顿一样伟大而又“阴魂不散”的力学大师。拉格朗日认为，流体的描述应该针对流场中的一团团流体，每一团流体都有自己的特性。流体团之间不能传递质量，但是可以传递动量和能量，即每一个流体团都是一个封闭系统。只要我们盯住流场中每一团流体的运动变化，就能够描述整个流场。这自然是可以的，也符合多数人的直觉。或者说，这种描述很像理论力学中的质点系。由于拉格朗日描述的研究对象是一个个封闭系统，每个系统的质量不变，因此可以直接应用守恒定律，得到对应的控制方程。不同时刻的流体团如图2.2 所示。

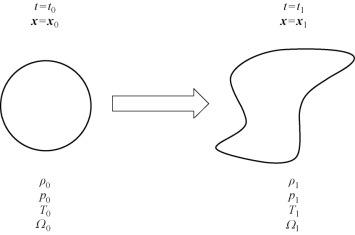
图2.2　不同时刻的流体团

虽然拉格朗日描述容易理解，也符合我们对事物的直觉，但是在具体使用时却存在诸多不便。对于生活中的许多流体动力学问题，人们往往并不关注流体中每个流体团的运动特性，而是关注不同时刻流场参数的空间分布。比如，我们洗完头之后用吹风机把头发吹干，并不关心具体哪一团流体在不同时刻究竟去了哪里，而是关注不同时刻头发周围空气的温度和速度分布。或者说，我们盯住的是某一个空间区域，而不是具体的哪一团流体。

基于这种想法，欧拉（没错，又是一个熟悉的名字）提出了著名的欧拉描述。欧拉认为，我们应该将流体流动的空间划分成若干个具有固定形状、固定位置的控制体，通过观察每一控制体内部的流体参数随时间的变化来描述整个流体的流动。这种描述方法本质上建立了一个物理场，即不同时刻、不同空间位置，对应着不同的流场参数。同一个控制体内，不同时刻对应着不同的流体团，如图2.3 所示。

拉格朗日描述和欧拉描述是针对同一个问题的两种描述方法，因此，二者之间必然存在着一定的转换关系。为了方便推导，我们选取某一个流体微团作为我们的研究对象，如图2.4所示。该流体微团在t 到 t + dt时间段内从控制体 A 运动到了控制体 B，空间位置从x 变为x+d x，对应的流体微团的参数φ 变为φ+dφ。由于两个时刻流体微团分别与两个微元控制体重合，因此，流体微团内参数φ 的变化dφ 应该等于两个微元控制体内参数φ 的差。那么，哪些因素会导致两个控制体内的参数φ 发生变化？首先，流场中不同位置的流场参数φ 是不同的，即使流场中φ 的分布不随时间变化，单纯移动位置也会使得对应的φ 不同。其次，一般而言，流场中各个位置的φ 实际上是随时间变化的，即使位置不动，同一位置不同时刻的φ也不同。可见，控制体内的流场参数会随着不同时刻流场的分布和控制体在流场中所处的位置发生变化。

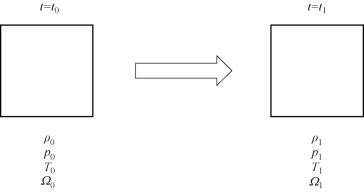
图2.3　不同时刻同一控制体内的流体参数(www.daowen.com)

图2.4　同一流体微团的运动

根据上述分析，在三维笛卡儿坐标系下，可以使用时间t 与3 个空间坐标（x， y ， z ）总共4 个自变量描述微元控制体内参数φ 的差异。我们可以得到

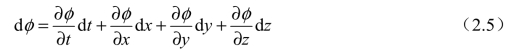
其中，方程左端为流体微团内参数φ 的变化量；右端为 td +t 时刻控制体B 与t 时刻控制体A内的参数φ 的差值。式（2.5）在数学形式上表现为全导数与偏导数的关系，说明拉格朗日描述与欧拉描述在物理本质与数学形式上都具有十分紧密的关系。对式（2.5）进行简单变形后可以得到

进一步将空间坐标对时间的导数转换为流动速度分量可得