许多平滑窗在过去的几年中被开发出来，其中许多都采用第一个提出它们的人的名字来命名。除了矩形窗之外，还有巴特利窗（Bartleet窗，是一个三角窗）、汉明窗（Hamming窗）、汉宁窗（也叫做Hanning窗或者Hann窗）、布莱克曼窗（Blackman窗，也叫做Blackman-Harris窗）、凯撒窗和丹夫窗（也叫做Chebyshev窗或者Dolph-Chebyshev窗）。它们中的一些特性如图9.4所示的时域图。

这些窗函数中的每一种窗的频谱形状和矩形窗频谱的形状（即sinc形状）都有点类似，因为都由主瓣和旁瓣组成。但是主瓣的宽度和旁瓣的幅度级对于每个窗都是不一样的。为给一个特定的频谱分析应用选择窗函数，有两个主要的标准供你使用。

在不同的DSP书籍中你可能要花大量的时间查到所有的窗函数的特性，而我们在表9.1中已经为你收集了最重要的通常使用的窗函数的指标。

与其他实际的DSP文章一样，表9.1列出了在归一化的弧度频率（这里π等于F_S/2）上的主瓣宽度值，N是窗函数的长度，并且旁瓣级单位为dB。我们没有显示所有定义的窗函数等式（这些在许多DSP理论书籍[2，15]中都能见到），因为我们将要讨论的是你需要利用Matlab怎样才能较容易地产生窗函数。

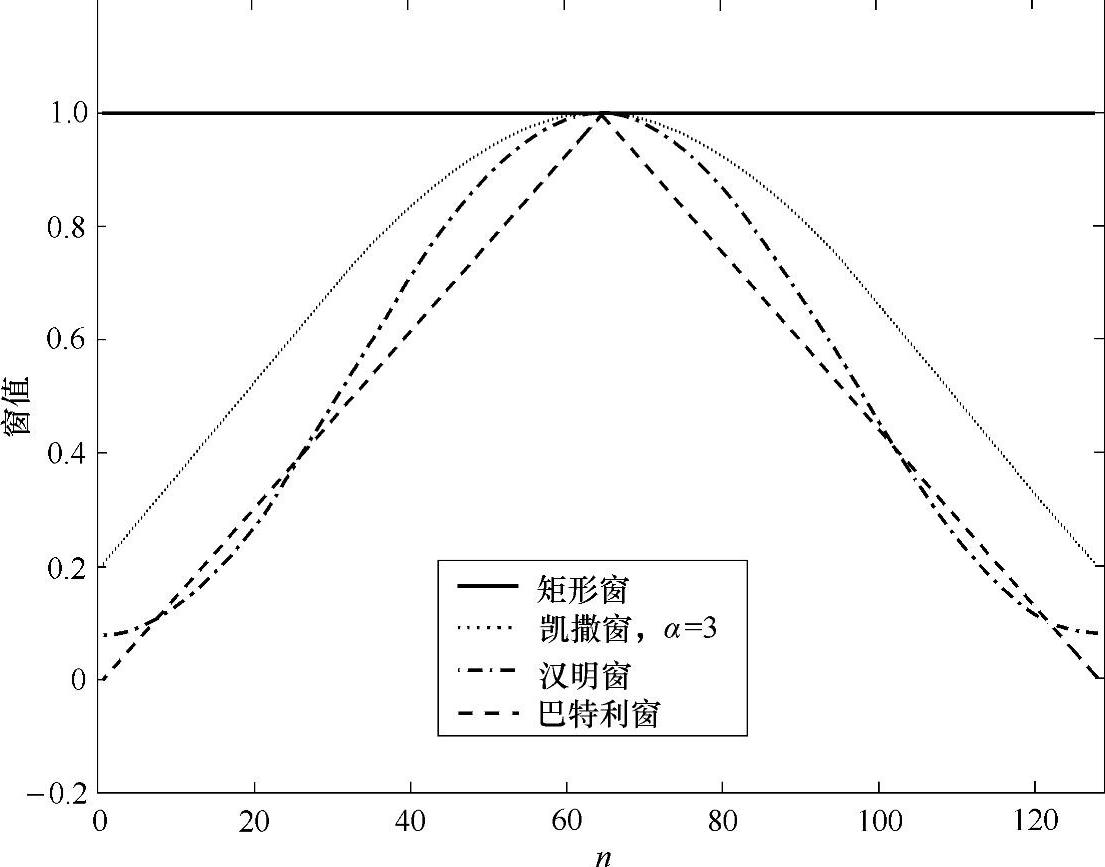
图9.4 时域中的几种窗函数 注意，在数据集的起始位置或者结束位置所有的这些窗都滑向零点位置，除了矩形窗函数。

对于频谱分析来说，在表9.1中仅有“主瓣宽度”和“旁瓣级”列是重要的。如果你利用窗函数的方法设计FIR滤波器，其他列也是有用的。这里还包括了一些额外的列，为的是在一个地方集中了所有的窗函数信息。在窗函数中我们最期望的是什么？①窄的主瓣宽度便于我们能够分辨相隔较近的频率成分；②较低的旁瓣级便于我们能够分辨靠近强信号的一个弱信号。令人遗憾的是，这是两个相矛盾的需求。花一些时间看一下表9.1，通常主瓣宽度（对于一个给定的数据长度N）会随着旁瓣变低而变宽。这一点也可以从图9.5中看到。此外，主瓣的宽度将会随着窗长度（它必须等于数据长度）变长而变窄——但是旁瓣级是不受窗长度约束的。像更多的工程决策一样，“最好”的窗函数选择将是根据你的特殊需要，对这些特性作一个折中。

三角窗函数的主瓣是我们能做到的“最好的”，因为半个主瓣宽度是2π/N=F_S/N。这是我们能够从N点的FFT中得到的最好的分辨率。但是，我们得到的三角窗的旁瓣级是比较糟糕的。对于频谱分析来说，其他的窗函数比三角窗更受欢迎。另一个我们应该避开使用三角窗原因是一个叫作“偏置”的现象。这里两个位置相近的频率成分的中心峰值出现的位置比它们实际位置要远（参考文献[1]是一个很好的例子）。使用一个普通的平滑窗代替三角窗可以消除这个偏置问题。(www.daowen.com)

表9.1 一个最为常用的窗函数特征的总结

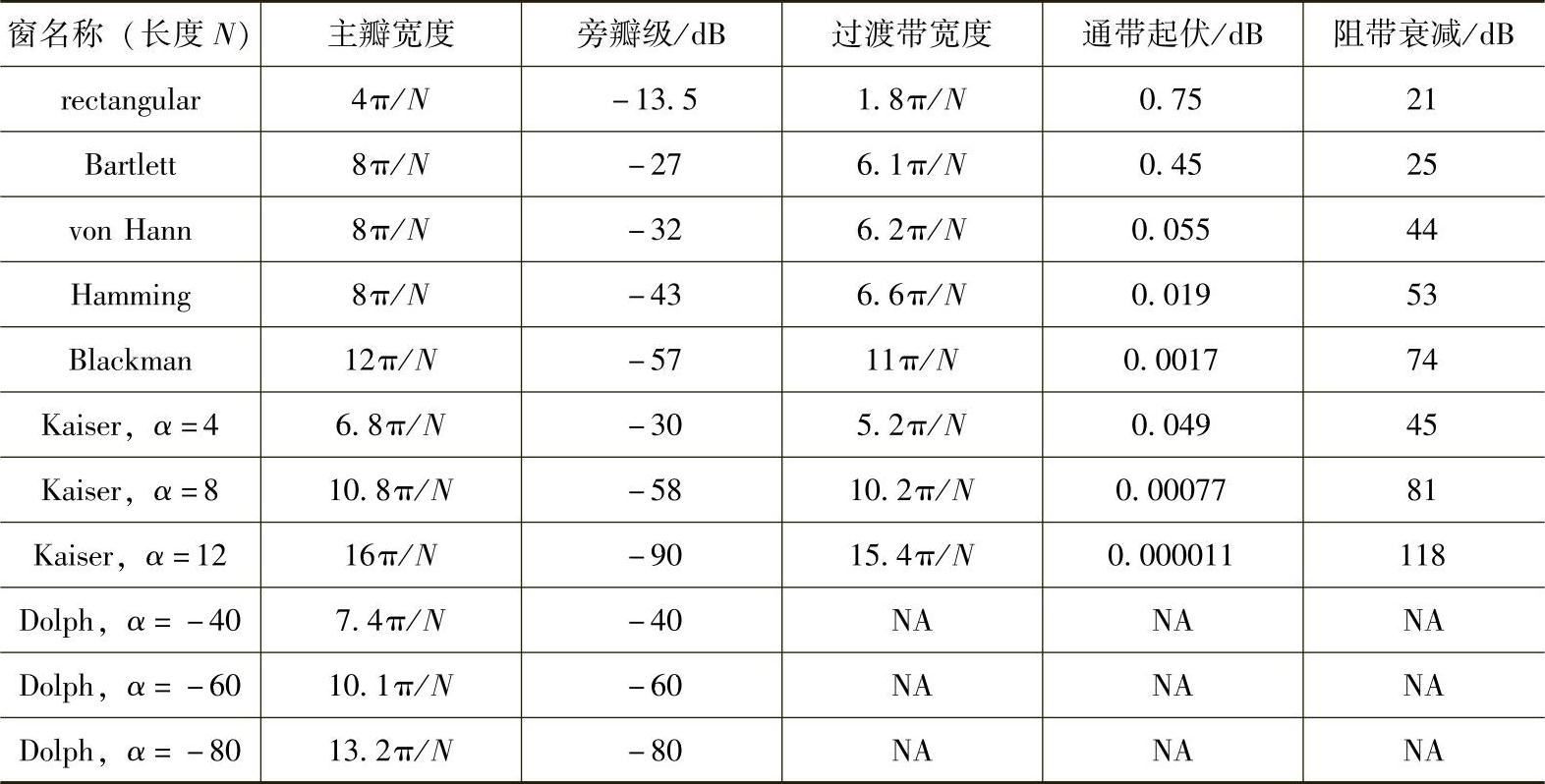
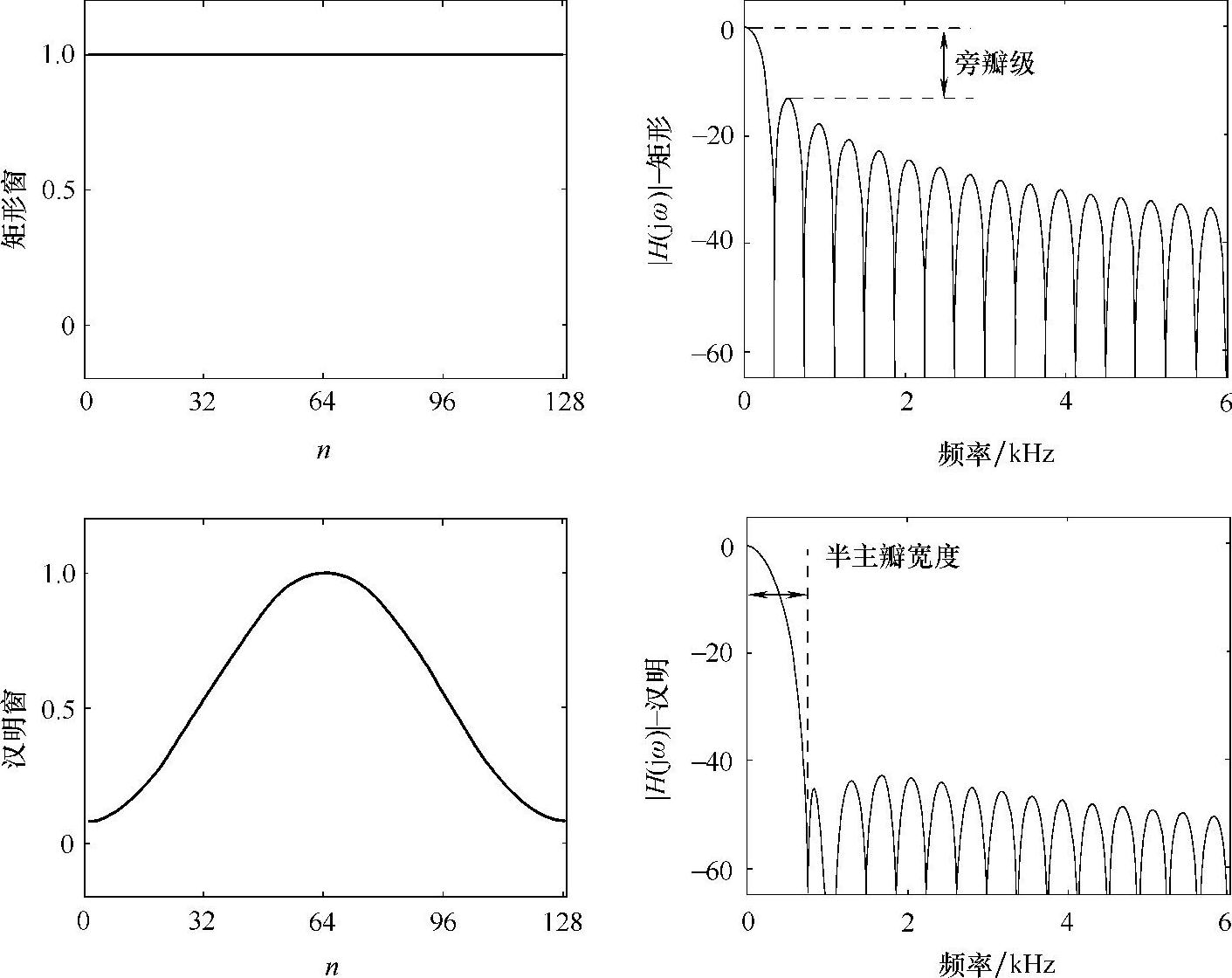
图9.5 两个窗函数的时域和频域比较 注意，一个窄的主瓣同时导致高的旁瓣级。

为了把加窗思想集中起来，让我们试验几个简单的例子。假定对一个信号进行谱分析，采样率是48kHz，我们期望的频率成分在14.0kHz并且另一个强度几乎相同的频率成分在14.1kHz。因此，两部分的频率分离间隔是100Hz。假设因为某种原因我们的数据帧长度将要刚好短于N=512，所以我们的窗函数长度就是N=512。我们想用一个平滑窗来消除这个偏离，而不想因为主瓣宽度太宽而把两个频率成分抹在一起。旁瓣级对于这个例子来说是不重要的，因为这两个信号的幅度量级几乎是相等的。我们能用汉明窗吗？从表9.1看出，汉明窗函数的半主瓣宽度是4π/N=2F_S/N=96000/512=187.5Hz，比相隔的两个频率间隔还宽，所以答案是否定的。我们不能使用汉明窗——它将把两个频率成分抹到一起——除非一些东西能够改变。惟一的窄窗是矩形窗，但是这样我们将遇到一个偏移问题。最好的选择就是增加帧的长度到1024点，这将把汉明窗的半主瓣宽度减小到93.75Hz，小于感兴趣的频率间隔。在这样的条件下，可以使用汉明窗。

现在假设第二个例子是和以前的一样的，但是在两个感兴趣的频率成分之间的幅度比率是100∶1（或者1∶0.01）代替前面的几乎相等的幅度关系。帧的长度依然是1024点，所以汉明窗不会把两个频率成分彼此分开。但是旁瓣怎么样呢？当幅度差别非常大时，我们就需要检查旁瓣级，单位为分贝。一个1∶100的幅度比是20lg（0.01）=-40dB。从表9.1中我们看到矩形窗、三角窗、汉宁窗不能区别这两个频率，而汉明窗可以，尽管我们把它削减的比较相近。布莱克曼窗在旁瓣级这点上是比较好的，但是它的主瓣宽度太宽。

从给出的这些例子，或许你能体会到处理思想变为选择一个合适的平滑窗。如果解决相近的频率量级是更重要的，我们趋向于选择一个较窄主瓣宽度的窗函数。如果分辨不同量级的频率成分更重要一些，我们趋向于选择一个低旁瓣级的窗函数。如果是离线使用，通常检查一个信号至少要用两个窗函数，一个有较窄的主瓣宽度，另一个有较低的旁瓣级。然而，如果使用实时的谱分析的话，我们就没有那么多的时间，所以在这样的情况下当我们选择窗函数的时候，不得不做出一个基于事实的折中。如果我们确实不知道在信号中隐藏的是什么频率和幅度，至少应该知道根据我们选择的窗口函数能够隐藏什么。