在许多情况下，为从FFT运算中获得好的结果，我们需要对每一帧数据使用一个平滑窗，如果对数据没有使用平滑窗，那么我们就是已经使用了有效的一个矩形窗，对于全部长度的数据来说，矩形窗有一个为1的常数值。

为什么事实是这样的呢？据FFT“所知”，所有的数据持续一个无限长的时间，用一个周期等于给定数据的周期来无限复现下去。当我们仅给出一个有限长度的数据（我们必须如此）进行变换，这与用一个无限长度的数据与一个有限长度的窗相乘是一样的，这个窗的常数值等于1。在图9.1所示的是一个比较形象的例子。为什么我们关心它呢？回忆一下，在时域范围内的乘法等于频域范围内的卷积。所以信号的频谱是窗函数的频谱与一个信号频谱的高效卷积，并且总是有某类窗存在——甚至是一个无意的矩形窗。矩形窗的频谱看起来像什么呢？

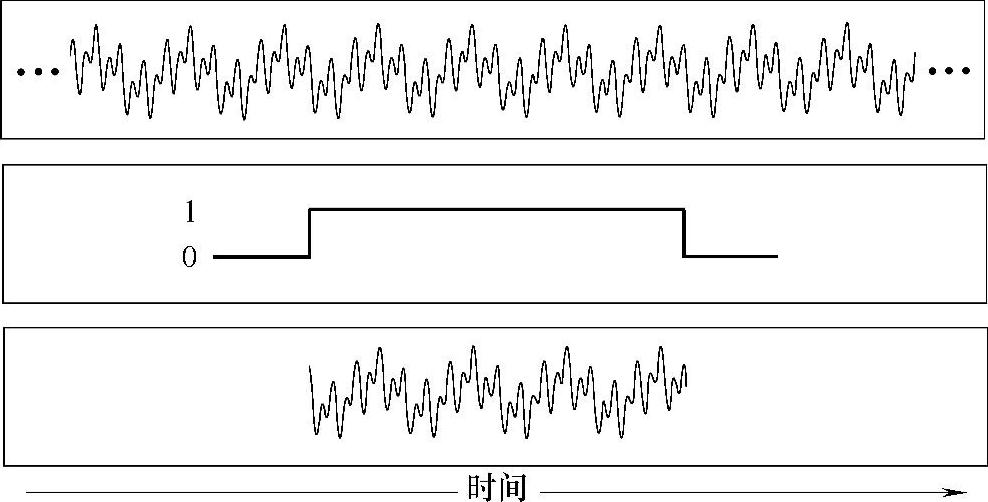
图9.1 使用矩形窗的时域效果（上：一个持续无限时间的信号。中：一个持续有限时间的矩形窗。下：这个无限 长信号和矩形窗相乘的结果是一个有限长的信号。）

一个矩形窗正好像一个信号的矩形脉冲（有时叫做“矩形函数”），在限定的时间区域上幅度为1，而其他地方值为0。可以回忆一下你的信号与系统课程，如果我们采用一个矩形脉冲的傅里叶变换，结果的频谱是一个“sinc函数”形状，这里“sinc函数”定义为sinc（πx）=sin（πx）/πx。另一个来自于傅里叶理论的有益的回忆是互逆扩展性，这告诉我们在这种情况下矩形脉冲变宽了，sinc函数波瓣的宽度变得更窄了。从这个方面来讲一个“较宽的”矩形脉冲相当于一个有较大N值的矩形窗（如一个有更多数据点的“较长的”窗）这个“rect↔sinc”的关系能够在图9.2中看到。

(www.daowen.com)

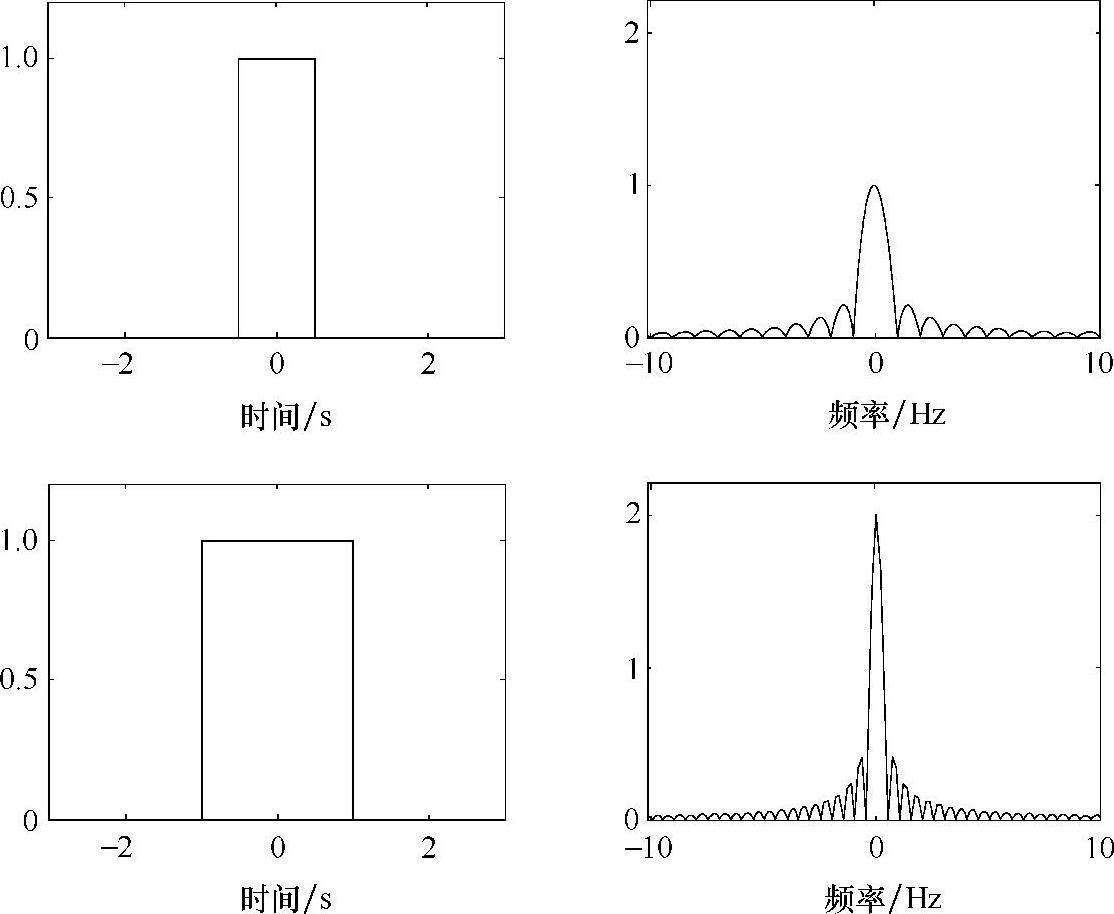
图9.2 “rect↔sinc”傅里叶变换对（左侧的两个图是时域中的矩形脉冲信号。右侧的两个图是傅里叶变换相应频谱的量级范围图。相位图没有显示出来。注意时域系统中的一个宽脉冲会导致 对应频域系统中的sinc函数的主瓣较窄。）

假设你对一个信号进行FFT，但没有首先对它使用平滑窗，然后再看使用矩形窗的作用。因为这个结果好像用这个信号的真实频谱与窗函数的频谱进行卷积一样，这个可观测的信号频谱不可避免地变得“模糊了”，如图9.3所示。

在图9.3的下图中，第一点的作用是明显的，在那里频率的“长钉”部分被抹成较宽的波瓣。如果两个频率成分靠得比窗函数的主波瓣的1/2还近，它们将相互“混合”，并且作为独立成分来区别它们将是不可能的。第二点的作用也可以在图9.3中的下图中看到，在这里k=18的频率成分是很模糊地通过来自于k=10的旁瓣。如果k=18的频率成分在幅度上被稍微衰减，它将被相近的旁瓣所“掩盖”。记住，我们总有一个窗函数应用到你的数据，对我们的数据如果没有明确地使用一个平滑窗，那么事实上我们已经使用了矩形窗。从上面的讨论中可知，显然我们需要知道可以使用的任何一个窗的两个关键特征：主瓣宽度和旁瓣级。

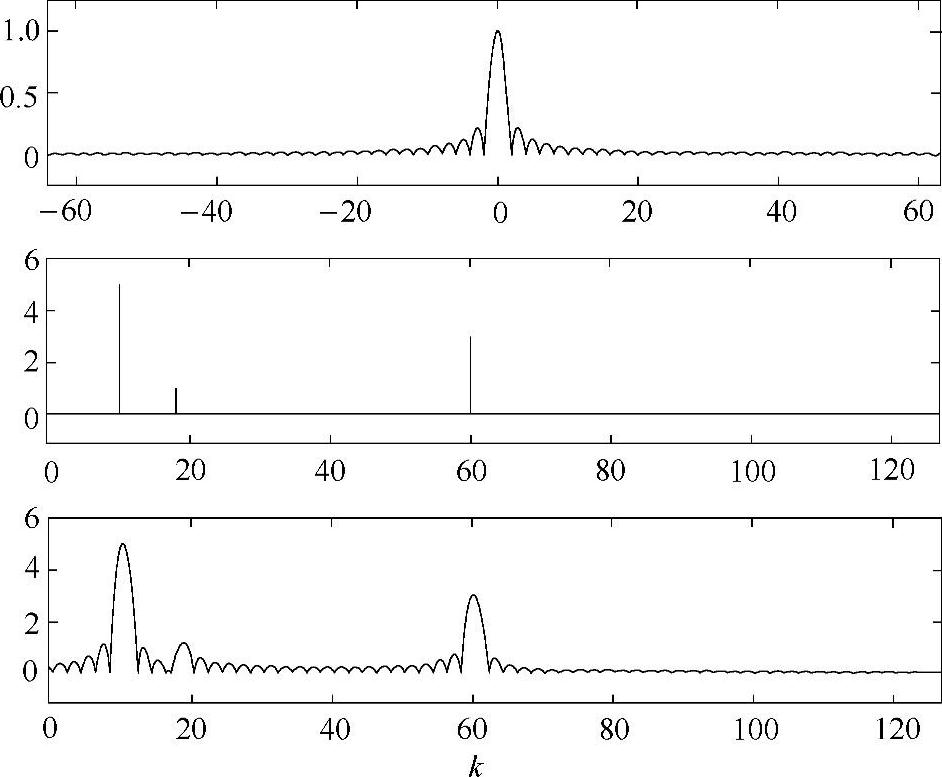
图9.3 应用矩形窗对频域的影响（上：矩形窗的频谱量级是一个sinc脉冲。中：某一个任意无限时域信号的限理论频谱（只显示正的频率部分），这个信号由3个频率组成，分别是k=10、k=18和k=60。下：窗函数的频谱和这个信号频谱的卷积结果。对谱分析来说，这有两个特别重要的推论可以在图中看见。第一，频率组成的最小宽度受窗函数频谱的主瓣宽度限制。第二，探测靠近强信号的弱信号能力受到旁瓣“高度”的限制（叫旁瓣级））