在本章，我们涉及了几个新的思想，也就是FFT和它的逆变换，通常的快速卷积，以及两种实时快速卷积的交叠方法。对我们来说，试图用一章的内容中覆盖它们所有的详细内容是不太明智的。我们所以选择集中到这里讨论，是为了帮助你们熟悉FFT。其他的概念留在接下来的练习中进行，并且如果你理解了FFT，对你自己来说，它们就很难使用。

为了确保我们正确地理解和应用FFT算法，我们可以在非实时的DSK上进行测试，像使用CPU一样使用DSK，并且把这个输出值和已知的正确值相比较。这个测试的C语言程序能够在本书CD中第8章的ccs\fft_example目录下。它并不意味着是一个最优的FFT程序，但它对于理解这个概念是很有用的。

在fft_example中的程序代码是相当简单的C语言程序。我们加入一个普通的“窍门”在这个程序代码中：因为FFT必须能够处理复数，而C语言不能直接支持复数，我们使用了一个结构体。即

程序清单8.3：为了在C语言中使用复数的结构体

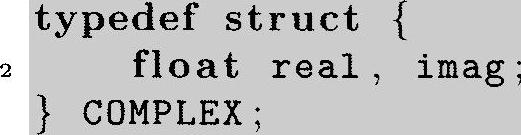
如果真的不需要双精度数据类型的全部精度，那么我们可以使用能够节省DSP的CPU的存储空间和提高处理速度的浮点数据类型。如果我们在PC上或者其他通用处理器上运行这些程序，也许对于这个结构体我们已经用到了双精度数。旋转因子的计算通过函数init_W（）实现。回顾旋转因子是W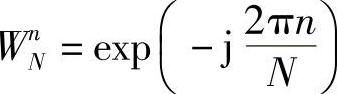。通过使用非常有帮助的欧拉公式从复数分解

e^jx=cosx+jsinx我们的函数init_W（）能够使用复数幂指数的三角关系等式，使这个旋转因子容易分解成实数和虚数部分。对于复数来说，用我们上面定义的结构体来转换这个关系非常好。函数init_W（）的应用见程序清单8.4，它只运行一次并且存储旋转因子的所有值，对于指定长度的FFT来说这是必需的。

程序清单8.4：一个计算复数旋转因子的函数

在上面的程序中，“N”是这个FFT的长度，“PI”在这个程序的前面有定义，“W”是这个复数的全矩阵。函数init_W（）产生W_Nⁿ需要的所有复数，这一点对你来说是非常清楚的。

对于FFT来说，实际的N点蝶形算法通过下面的代码执行，代码摘录于fft_c（）函数。

程序清单8.5：执行FFT蝶形运算的C代码

(www.daowen.com)

输入数据在x矩阵中，这个矩阵是由复数数据类型元素组成的，与前面讨论的结构体定义一样。并且旋转因子通过指针“u”进行存取。变量“len”用于依次地把数据集合分割分成两半（见清单的第3行）。其余的行仅仅执行了蝶形算法需要的加法和乘法运算。你应该用少量的数据元素（如N=8）来运行你自己的算法，经常回顾一下相称的蝶形图（见图8.5）。

最后，因为蝶形图传出的数据是位码倒置的顺序，我们需要重新排列这些数据返回到“正常的”顺序。这依靠“解析”矩阵“x”的元素来实现，这里指的是FFT运算后结果的转换，而不是输入数据的转换，这个转换算法通过下面的程序代码来实现。

程序清单8.6：一个从位码倒置到正常顺序转换的“解析”程序

既然你理解这些代码，回到前面并且复制这个工程的全部文件到一个单独的目录中。注意，这是一个非常简单的程序，没有实时性的要求，所以这个工程非常小。准备好后，在CCS中打开这个工程并且单击“Rebuild All”。一旦构建完成，单击“Load Program”加载程序到DSK板并且单击“RUN”。这样程序就会在DSK板上运行，并且输出结果能在CCS界面底端的StdIO窗口中看到。

为了使事情尽可能简单，输入数据是硬编码后输入到程序文件中，如“x={0，1，2，3，4，5，6，7，0，0，0，0，0，0，0，0}”。这意味着你将计算一个16点的FFT。根据我们的一些傅里叶变换知识，能够很容易地预测出FFT结果数据的以下几个特点：①因为输入数据的均值非零，频域内的DC（即0Hz）值也会是非零值；②因为有16点的输入值，那么我们将会获得16点的输出值（尽管输出值将包含16个复数）；③因为输入数据是实数，输出数据将是关于F_S/2点对称的。虽然你可以自由地改变输入数据或者调整代码以接收作为这个函数的一个参数的输入数据。我们用这种方式写它以便于你们容易地检查这个算法的正确性。你需要做的全部事情是比较运行在DSK板上的C程序结果和Matlab命令结果。

程序清单8.7：用于确认你的FFT正确性的Matlab命令

在第2行的末尾我们用转置矩阵运算（，），这样输出将排列成较好的列形式。Matlab命令窗口显示的结果如下：

这些数据在本质上与在DSK板上通过运行C语言代码得到的FFT结果是一样的。不但是我们的算法函数正确，而且我们预测的关于FFT的结果也是可以验证的。DC值非零（28.000），有16个输出值，并且每一边的F_S/2值（这里的F_S/2值在X[8]=-4.000处）是对称的。再随意试其他的输入数据集合并且和来自于Matlab的结果相比较。

与我们这里讨论花费的篇幅比起来，FFT将会有更多应用和结果说明。在本书第9章的谱分析部分我们将再次涉及这个题目。