在蝶形图左边输入值的顺序对你来说也许有些陌生。依靠计算机运行时间抽取FFT计算，从而获得高效率的蝶形算法，输入的值必须重新排列成众所周知的位码倒置形式。你知道为了给一个N=2ⁿ的FFT输入矩阵的N值指出地址（或索引），就需要n比特（如果这个索引值展开成二进制形式）。对位码倒置来说，数据矩阵元素的二进制索引号在输入端是左右倒置的。例如，在图8.5中，你可以认为第二个输入元素是x[1]。有索引号扩展为一个3比特二进制值就是x[001]，导致索引号的比特值就是x[100]，它在十进制符号表示中是x[4]。这是实际的第二个输入元素在位码倒置后的位置。时间抽取FFT的对偶操作是频率时间抽取FFT。在蝶形图中惟一的区别是，对于频率抽取FFT来说蝶形部分的顺序是倒置的，旋转因子交换位置，并且输出值早于输入值出现在位码倒置的顺序中。这并不是说本质上时间抽取FFT优于频率抽取FFT，并且实际的选择是具有典型地随机性。

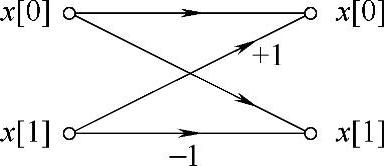
图8.3 时间抽取基2的FFT蝶形图，N=2，未标注支路的增益+1

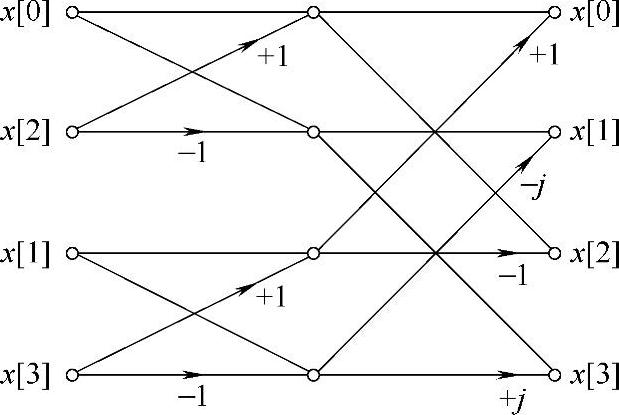
图8.4 时间抽取基2的FFT蝶形图，N=4，未标注支路的增益+1(www.daowen.com)

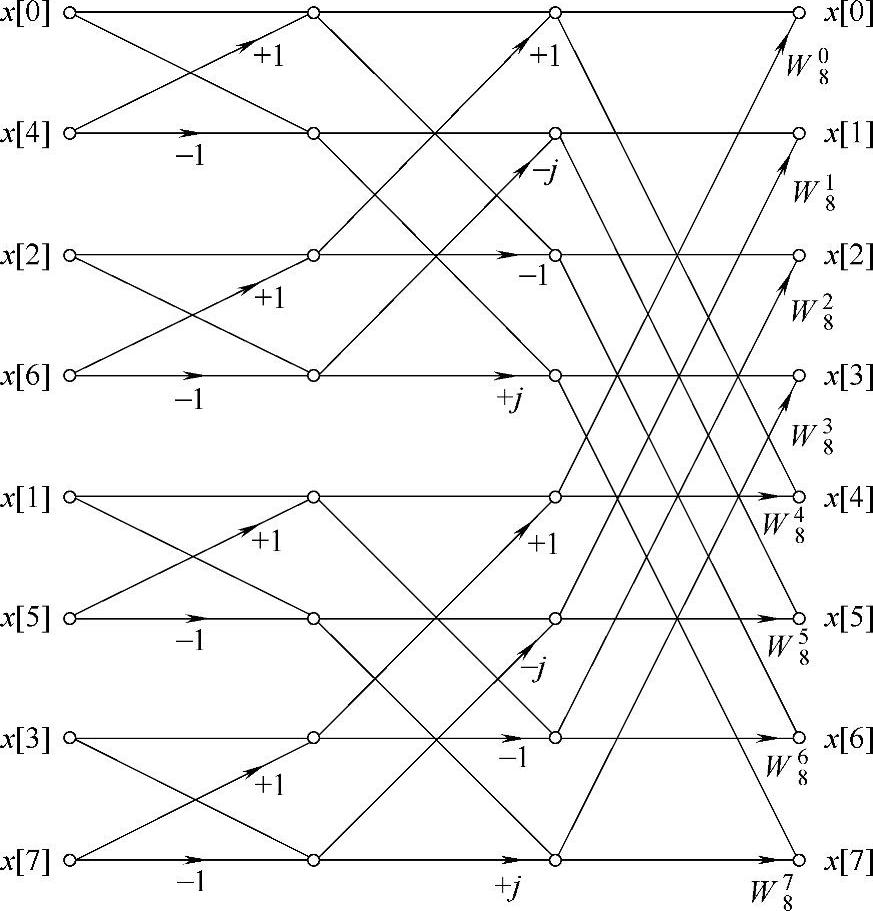
图8.5 时间抽取基2的FFT蝶形图，N=8，未标注支路的增益+1

当我们在蝶形算法的任何一个输入边或者输出边使用位码倒置时，我们能够执行叫作“in-place”的运算。这意味着相同的矩阵保存输入数据也用于保存输出数据。位码倒置确保不会让输入元素被输出元素的值所覆盖，除非不再需要执行更多的FFT运算。