经过Cooley和Tukey发展了FFT以后，主要思想是当DFT的长度N不是一个质数时，这个运算能够拆分成一些短的DFT，对于所有的短长度DFT运算需要的全部乘法和加法总数小于单一全长度的DFT运算的乘法加法数。每一个这些长度较短的DFT能够接着继续拆分成许多偶数个短DFT，依此类推，直到最终DFT的长度是一个质数因子N。

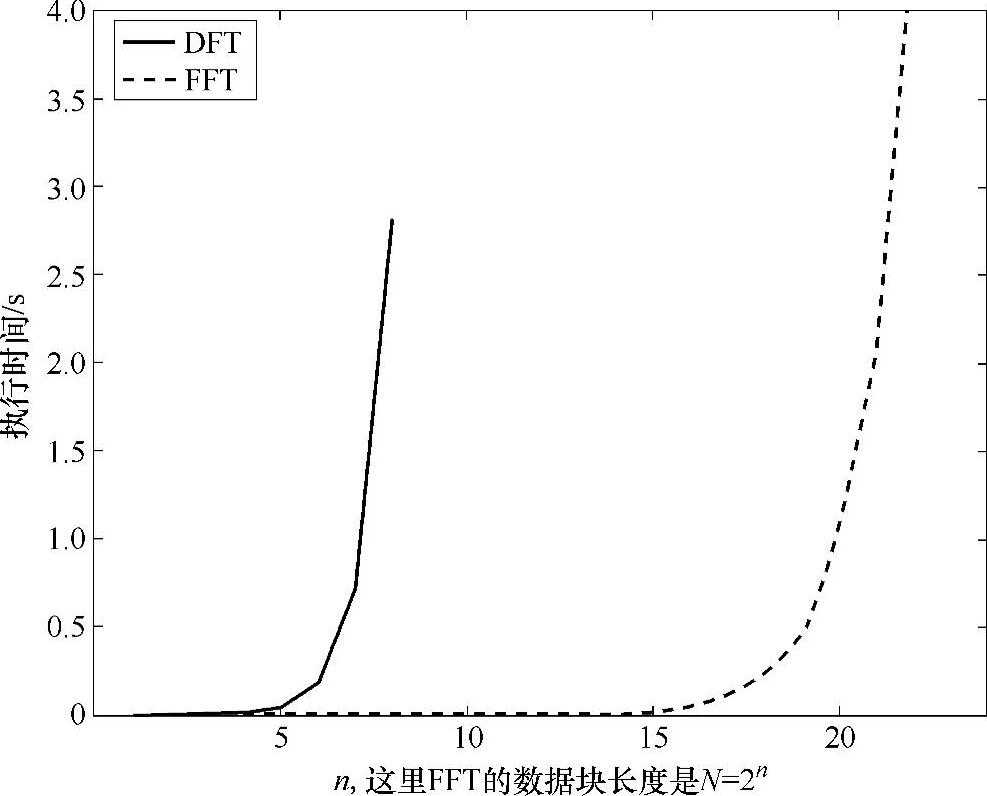
然后，这些最短的DFT使用常规方法计算。对应的阶数可以使用，以最小的DFT开始并且构造（重组）成一个大的DFT。对于基2的FFT（常见的类型），FFT的长度必须是2的幂。假如一个N=8的例子，FFT将要拆分成2个4点的FFT，每一个4点的FFT又要拆分成2个2点的FFT（因此一共有4个基2的FFT），这样来完成计算。或者说它将执行4个2点的DFT，用这些结果计算2个4点的DFT的最终结果。前面的方法叫做频率抽取算法，后面的方法叫做时间抽取算法。用合适的求和及重新使用中间的计算结果，也就是利用旋转因子的周期性。与“brute force”DFT比较起来，这种FFT算法能够大幅提高计算效率。计算N点的DFT需要相应的复数运算的计算量为N²，同样的计算N点基2的FFT需要相应的复数运算的计算量为Nlog₂N。这样对于一个512点的例子中，DFT将自然需要262114次复数运算，而FFT将仅需要4068次复数运算——这比DFT快了5倍多。对于更大的DFT运算这种差别更加明显。在典型的计算机上运行FFT，根据经验的加速情况如图8.2所示。注意，从图上看FFT执行N=2²⁰=1048576数据点的DFT时间和“brute force”DFT执行N=2⁷=128数据点的时间相同，也就是说快了8192倍。这就是FFT得到广泛使用的原因。

(www.daowen.com)

图8.2“brute force算法”的DFT相对可商用的基2的FFT程序有关的计算时间曲线（图上绘出的是来自于桌上工作站的平均经验值）

传统表示FFT算法的方法是使用“蝶形图”，它描述了分解、中间的求和及旋转因子的使用。2点、4点、8点时间抽取FFT的表示方法如图8.3、图8.4、图8.5所示。通过小的蝶形图来手工描绘算法是非常有益的，能帮助你计划下一步该怎样进行。