作为地质统计学研究的一种最基本的工具，变异函数在一维条件下定义为，当空间点x在一维轴上变化时，区域化变量Z（x）在点x和x+h处的值Z（x）与Z（x+h）差的方差的一半定义为区域化变量Z（x）在x轴方向上的变异函数，记为γ（x，h），即

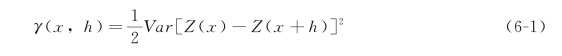
式中：γ（x，h）为空间点x与矢量h的半方差函数；Z（x）、Z（x+h）分别为点x、x+h处的样本值。

当变量满足二阶平稳假设时，对任意的h有

因此，式（6-1）可以写成

由式（6-3）可看出，变异函数只取决于x与h两个变量，当该函数与位置无关而仅依赖于h时，γ（x，h）可改写为γ（h）。即(www.daowen.com)

通常将γ（h）称为半变异函数（Semivriograms）。

一般情况下，理论变异函数模型是未知的，通常要利用实际取样的样本值去估计，对向量h而言，可以计算出一系列的γ#（h）值。现阶段，地统计学模型主要分为3大类：第一类为有基台值模型，包括球状模型（Spherical model）、指数模型（Exponential model）、高斯模型（Gaussian model）、线性有基台值模型（Linear with still model）、纯块金效应模型（Pure nugget effect model）；第二类为无基台值模型，主要有抛物线模型、幂函数模型以及线性无基台值模型；另外，有一类还被称作空穴效应模型。图6-1常见变异函数图为常见几种模型的变异函数图，表6-1为相应的空间变异模型。

表6-1　常见变异函数模型

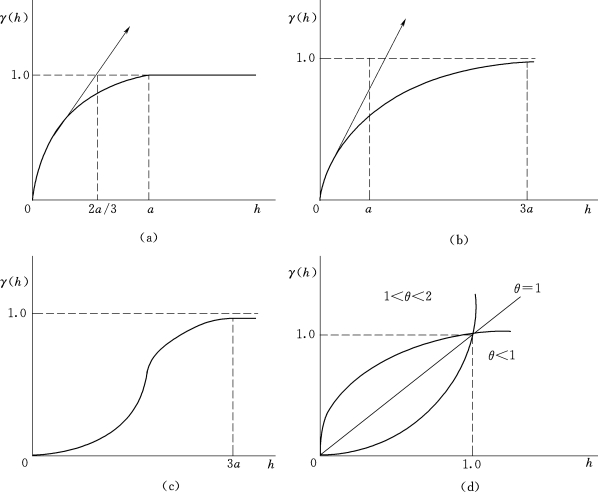
图6-1　常见变异函数图

（a）球状模型；（b）指数模型；（c）高斯模型；（d）幂函数模型