交汇锋是双点源发生交汇的地方，在双点源连线的中间并与双点源连线垂直，它是个瞬时零通量面。湿润锋发生交汇后，主要是重力势起着主要作用，那么水分运移主要是向土壤垂直下方运移。对于小的滴头流量，入渗能力较弱，在相同间距和灌水量条件下，所需入渗时间较长，水分受到重力势能的影响显著，那么向下运移的垂直距离就越深，交汇湿润锋水平宽度推移就显得缓慢。

在相同灌水量（10L）下，不同滴头流量的湿润锋在交汇处的剖面如图5-4所示。

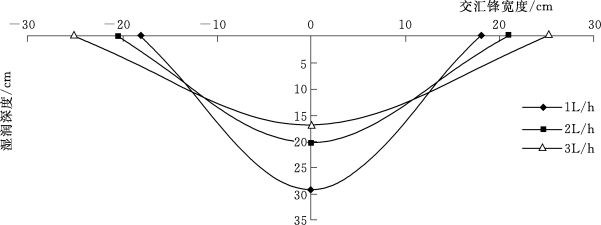
图5-4　不同滴头流量的交汇湿润锋剖面

图5-4中0点表示交汇中心，交汇湿润锋垂直与两个单点源的连线。在累积入渗量10L的条件下，不同滴头流量的水平交汇宽度和入渗的垂直深度都具有差异，其中1L/h滴头流量下，交汇湿润锋水平宽度和垂直深度分别为18cm、29.1cm。3L/h的滴头流量下，交汇湿润锋水平宽度和垂直深度分别为25.25cm、16.9cm，2L/h的交汇湿润锋特征在它们之间，由此表明在交汇区，滴头流量小的交汇锋在垂直方向运移距离较深，水平宽度较窄，大的滴头流量表现正好相反。实验中可以发现，交汇区界面形状近似于椭圆形状，交汇区剖面则近似与抛物线状，当两个单点源湿润锋发生交汇后，形成的交汇湿润锋延续着水平和垂直运移，随着入渗时间的增加，交汇锋的水平和垂直运移距离逐渐增大，但在相同入渗时间内，交汇湿润锋垂直运移速率要大于水平运移速率，这是因为入渗垂直方向受到基质势和重力势的作用，而在水平方向只受基质势的作用，两个单点源的湿润锋运移方向是相向的，形成了湿润锋相互挤压，也造成了交汇锋在水平方向上运移速率减小。

不同的滴头流量具有不同的湿润锋运移速率，那么两个点源湿润锋交汇所需的时间就会不同。滴头流量小，湿润锋移动速率较慢，那么到达交汇的时间就较晚，相反较大的流量，湿润区交汇的时间就早，例如3L/h的滴头流量需要40min交汇，2L/h的滴头流量却需要65min交汇。表5-3中入渗时间分别是3h、6h，不同滴头流量的双点源交汇湿润锋宽度的实测值。可以得出：相同滴头流量下，入渗时间越长，灌水量越大，那么交汇锋的宽度就越大，交汇时间随着滴头流量的增加而提前。

表5-3　不同滴头流量下交汇湿润锋宽度与入渗时间

湿润锋发生交汇后，交汇界面的运移速率要快与滴头处中心运移速率，达到一定入渗时间以后，交汇界面的湿润深度与滴头中心处的湿润深度大致相等，底部湿润锋与滴头处接近水平线。(www.daowen.com)

双点源交汇湿润锋运移距离与入渗时间的拟合关系如图5-5所示。

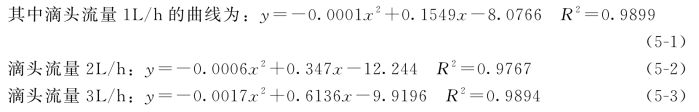
上述拟合曲线的相关系数较高，均大于0.97以上，说明交汇界面水平湿润锋运移距离与入渗时间之间具有良好的多项式关系。

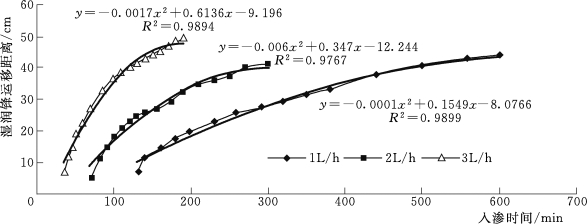
图5-5　双点源交汇湿润锋运移距离与入渗时间的拟合关系

在双点源入渗发生交汇之前，各单点源入渗的湿润锋形状近似于半椭圆形状，与自由入渗情况下的湿润锋形状相同；双点源发生交汇后，随着入渗时间的延长，双点源入渗的湿润锋相连、重叠，且交汇界面的湿润锋运移速率要大于单个点源中心处湿润锋运移速率，达到一定入渗时间后，交汇界面处的湿润深度与单点源中心处湿润深度基本相等，湿润锋接近于水平线。

图5-6为在双点源流量为3L/h的条件下，交汇区湿润锋速率与单点源中心湿润锋速率的对比。从图中可以得出：入渗初期的湿润锋运移速率递减梯度较大，随着入渗时间的推移，入渗湿润锋运移速率梯度变小。经前面分析可知湿润锋运移距离和入渗时间具有良好的幂函数关系，可推出湿润锋运移速率也与入渗时间成幂函数关系。若u 1为交汇界面湿润锋运移速率，u 2为单点源中心湿润锋运移速率，在相同的入渗时间里，u 2＞u 1。即双点源发生运移速率要快于点源中心处水平湿润交汇之后的入渗阶段，交汇面处湿润锋运移速率，但到了一定入渗时间后，滴头与湿润锋的距离较远，水分受到土壤吸力减小，所以入渗速率和前段时间相比减小，逐渐趋于稳定。

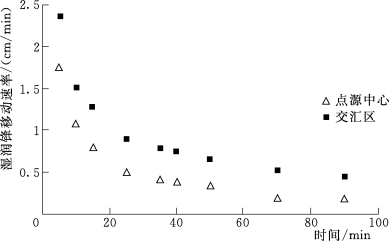
图5-6　单点源与交汇区的湿润锋速率对比