从上述分析，Laplace算法的核心思想是将表示图像的二维矩阵根据Laplace算子进行9点差分运算，在本算法中，初始矩阵和目标矩阵位于不同的内存区域内，因此每个元素的Laplace变换不存在读写依赖关系，可以并行执行，符合GPU大规模并行执行的特点，而且该算法属于访存密集型。对此本章通过提高访存效率，合理使用GPU硬件资源对算法进行优化。

在Laplace算法中，每一个元素的变换都需要从初始矩阵中读取自身及周围的8个元素。然后根据Laplace算子进行8次加法和9次乘法运算。除此之外，还需要9次的迭代计算和10次的地址计算，而每次地址计算都需要1次字符数乘法和加法计算。最后将计算结果写回目标矩阵。由于Laplace算子矩阵规模较小，可直接放在具有极高访存带宽的片上常量缓存中，所以计算密度不需要考虑Laplace算子矩阵的读入操作。再者Laplace算法本身具有数据重用特性：如图5-33所示，矩阵元素（1，1）进行Laplace处理时，需要加载（0，2）和（2，2）两个矩阵元素，而这两个矩阵元素在对矩阵元素（1，2）进行Laplace变换时也需要用到。因此，使用本地内存实现数据本地化，以提高算法的计算密度和数据重用，是提高Laplace算法性能的重要方法。

图5-33 Laplace算法的基本原理(www.daowen.com)

每个线程负责计算一个目标矩阵的元素，通过中心元素来确定坐标位置，并读取8个边界元素。这种初步实现算法容易实现，但是由于global memory访存效率不高，以及相邻两个点的计算是需要重复读取6个元素导致访存片外内存的开销增大，如图5-34所示。为了提高算法的性能，还需通过了解算法特性和底层硬件资源特征，实现两者的有效映射。

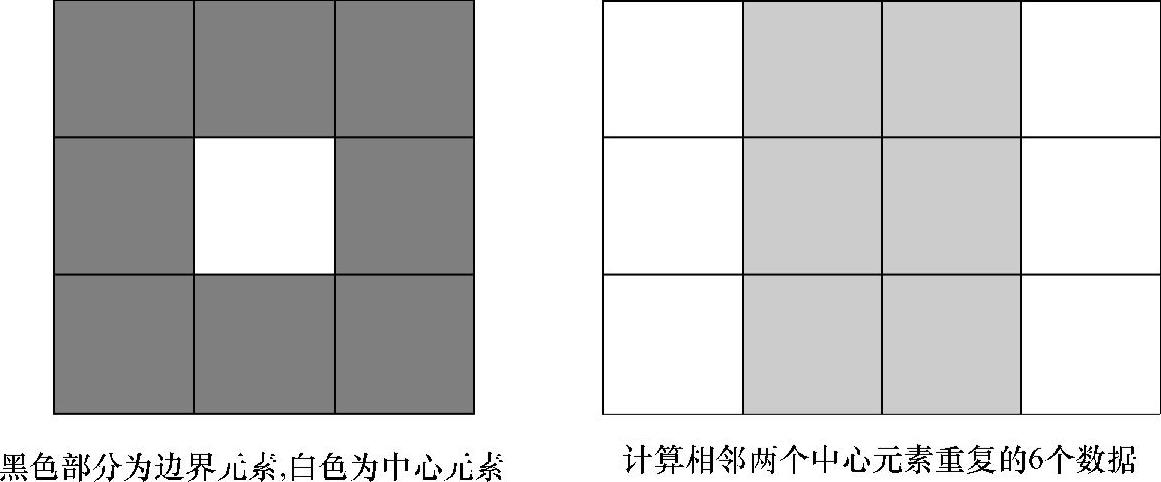
图5-34 Laplace算法分析图