1.resize算法简述

从5.5.1小节分析可知，resize算法在不同的需求驱动下所采用的插值方式并不相同，而最近邻插值方式与双线性插值方式为两种基本的插值方式，最近邻插值方式依据公式（5.1）进行实现，由于其实现较为简单，只需要直接在src中进行取数计算，然后再往结果矩阵进行写入即可，相关的访存过程和计算过程与双线性插值方式并不存在实质性差别，为了节省篇幅，把焦点更好地集中于优化方法本身，本章将重点对双线性插值方式进行剖析，而对于简单的最近邻插值方式只给出其基本的并行实现，读者可依据本章对双线性插值方式的优化方法推广至最近邻插值。

下文的resize算法主要基于双线性插值方式的并行实现。

双线性插值法的基本实现可概括为以下三个步骤：

目标图像像素点在源图像的坐标定位。

定位坐标周边四个元素的读取与权重分配，依照公式（5.2）计算目标图像像素值。

把结果值写入目标矩阵。

虽然双线性插值方式之间不存在数据依赖，但对数据的读取位置随着目标图像大小与源图像大小的比例变化而变化，一定程度上加大了并行程序通用性的编程难度，由于一个线程需要读取两行的四个像素点数据进行运算，因此访存方式并不规律，不恰当的访存可能会增加延迟而导致性能的下降。下面将给出最近邻插值方式与双线性插值方式的resize算法的基本实现，并主要针对双线性插值方式对resize算法进行优化，通过增加每一个线程所处理像素点的个数以及对访存方式的优化，以追求更高的性能。

2.resize算法基本实现(www.daowen.com)

基本实现的resize算法线程与像素点对应关系为一对一，如图5-23所示，即一个线程负责一个像素点的运算，通过坐标的映射关系寻找目标图像像素点对应于源图像像素点的映射关系，从而实现图像的缩放。

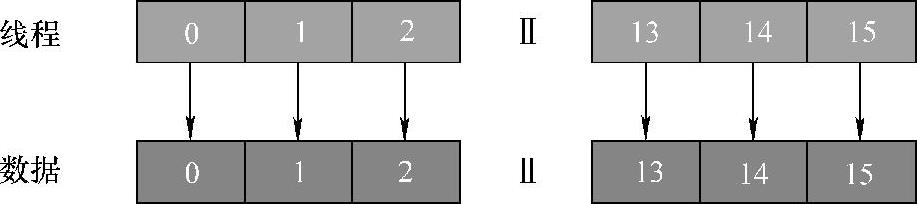
图5-23 基本实现的线程-数据对应关系

此版本的源图像为512×512规模，目标图像为1024×1024规模，深度为5，在通道1和通道3的运行时间分别为0.0594ms和0.1579ms。

同样，下面给出双线性插值方式的resize算法的基本实现，一个线程负责图像的一个像素点的运算，以深度为5为例，此版本在通道1和通道3的运行时间为0.1322ms和0.0.3892ms。

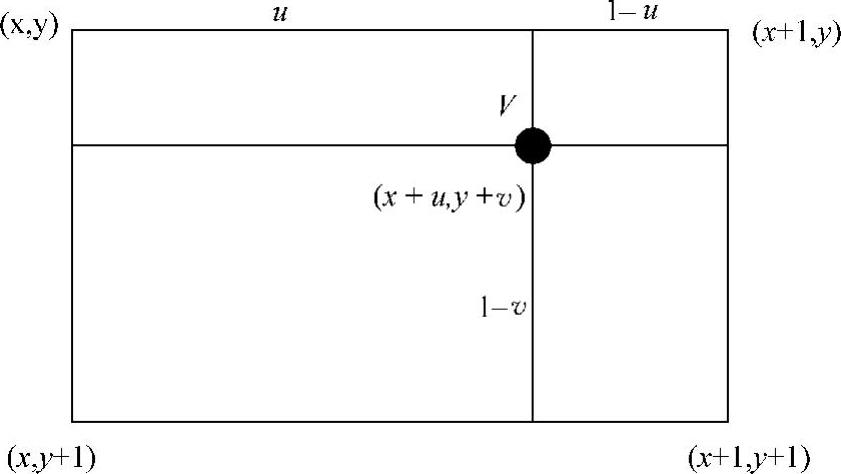
图5-24 双线性插值坐标及权重关系

如图5-24所示，当目标图像（X，Y）坐标在源图像的计算结果坐标为（x+u，y+v）时，即图中黑色点处，结合图解和公式（5.2），可以得出，源图像点（x，y）对于目标图像（X，Y）的X方向及Y方向的贡献权重分别为（1-u）和（1-v），同样，（x+1，y）对于目标图像（X，Y）的X方向及Y方向的贡献权重分别为u和（1-v），而（x，y+1）的贡献权重为（1-u）和v，（x+1，y+1）的贡献权重则为（u，v），通过对四点的像素值乘以其两个方向上的贡献权重，累加求和，得出目标像素点的像素值，并最终写入至目标图像。