本节实验运行的GPU平台为AMDFirePro^TM W8000，主频0.88GHz，有1792个core，28个CU，带宽176GB/s。

本节对5.4.2小节的Naïve版本以及第4章提及的4种优化策略进行性能的总和对比，若优化策略存在多种实现思路，将性能最优的为准则参与对比，性能总和对比如图5-17所示。

图5-17为并行规约求和算法不同版本之间的算法性能对比。并行规约求和算法经过多种优化策略的步骤性优化，其执行时间从最初的Naïve Reduce的1056.199μs降低至417μs左右，性能提升了约60.52%。

根据图5-17性能数据可知，work-group内规约优化算法相较于Naïve版本，work-group内规约优化算法通过解决local memory的bank conflict和wavefront内部线程的条件分支，有效地提升了local memory的访问效率及wavefront内部线程操作的并行性，因此性能上优于Naïve版本。work-group内规约优化算法性能较Naïve Reduce提升了17.58%。

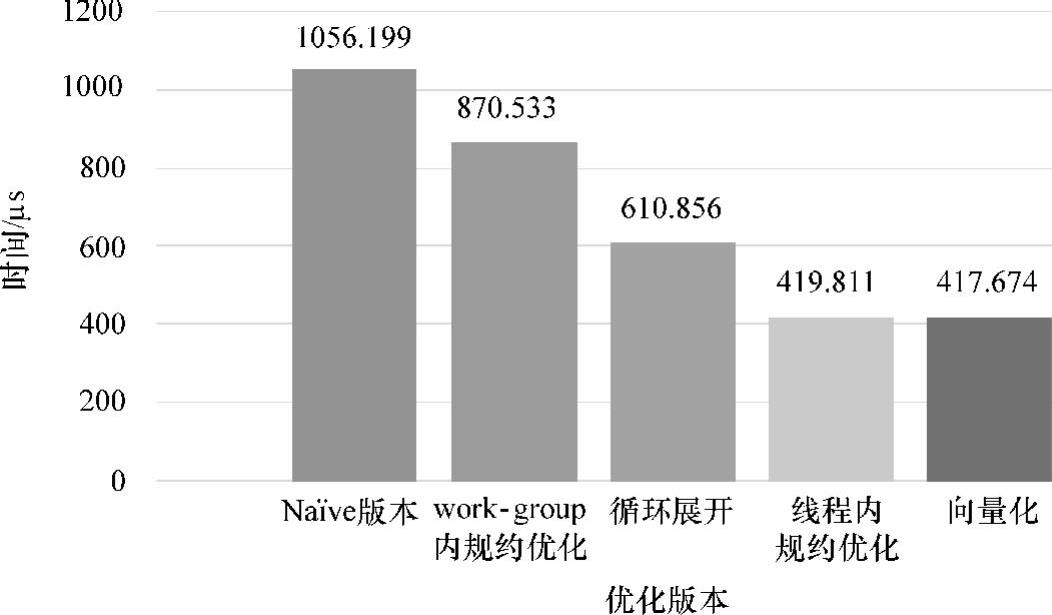
图5-17 并行规约优化算法性能综合对比

循环展开优化算法是在work-group内规约优化版本的基础上结合硬件调度和执行单元wavefront的特点进行优化的算法版本，循环展开优化算法对work-group内规约过程进行循环展开，以减少规约过程的本地同步操作，进而减少时间开销，根据图5-17可以得出，循环展开优化算法相对于work-group内规约优化版本在性能上得到提升。

线程内规约优化算法基于循环展开优化算法，在对work-group内规约完成优化的基础上，对线程内的规约过程进行优化。循环展开优化算法在第一次规约时就有一半的线程处于空转，只有一半的线程进行规约操作，大大浪费线程资源。线程内规约优化算法在把global memory的src数组加载进local memory的ISum数组过程中进行第一次规约操作，所有线程均参与规约操作，每个线程对两个或多个的数据进行规约，因此更充分地利用了线程资源。此外，当每个线程处理times个数据时，所需的全局线程数减少至数据总量DATA_NUM的1/times，从而减少work-group数目，最终减少了局部和累加的原子操作。因此，其性能相对于循环展开优化算法得到有效的提升。

向量化优化算法同样是以循环展开优化算法为基础进行的线程内规约优化，然而向量化优化算法与线程内规约优化算法在性能上相差无几。其原因在于本次实验GPU平台为AMDFirePro^TM W8000，基于GCN架构的AMD FirePro^TM W8000弃用传统的SIMD流处理器阵列，取而代之的是GCN阵列，不再对向量操作进行加速，其对向量化的操作将会拆分成多个标量操作进行，因此，编程中的向量化操作对性能的提升效果十分有限。在GCN架构的GPU上，向量化优化算法与线程内规约优化算法其优化本质是相同的，只是规约数据之间步长不同，因此两者性能十分相近。

将并行规约算法与串行规约算法在不同的数据规模下进行对比，以加速比（串行规约时间/并行规约时间）作为评价基准。

本小节的实验使用g++编译器在编译过程对串行规约算法Serial Reduce进行了优化，采用了“-O3”最高优化等级。在数据规模为4096×4096情况下，Serial Reduce优化前规约时间为43687μs，对比5.4.1小节所示，在采用“-O3”选项后，其规约时间下降至8077μs。

根据图5-18可知，当数据规模较少时，如64×64，串行规约算法优于并行规约算法，因为这种情况下并行规约算法在数据传输时间高于计算时间，甚至不足以隐藏存储操作的延迟，因此性能较差。然而随着数据规模的增大，并行规约算法的优势开始显现。在1024×1024数据规模下，加速比逼近20。

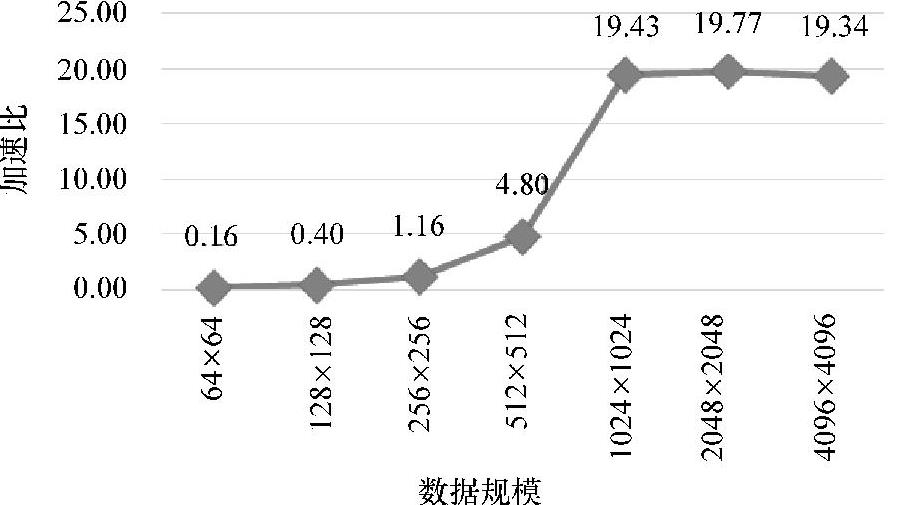
图5-18 加速比（串行规约/并行规约）

循环展开算法性能如图5-19所示，Completely-Unroll Kernel相较于Last-Wavefront-UnrollKernel的性能上并没有提升，甚至略低于Last-Wavefront-Unroll Kernel。分析可知，在NVIDIA的GPU上，因为每一个block最大可开启线程数目为1024个（AMDGCN架构的GPU为256个），因此可以对for进行更多次的展开，展开过程在编译阶段已经确定了，因此Completely-Unroll Kernel会有比在GCN架构的GPU上有更好的优化效果。(www.daowen.com)

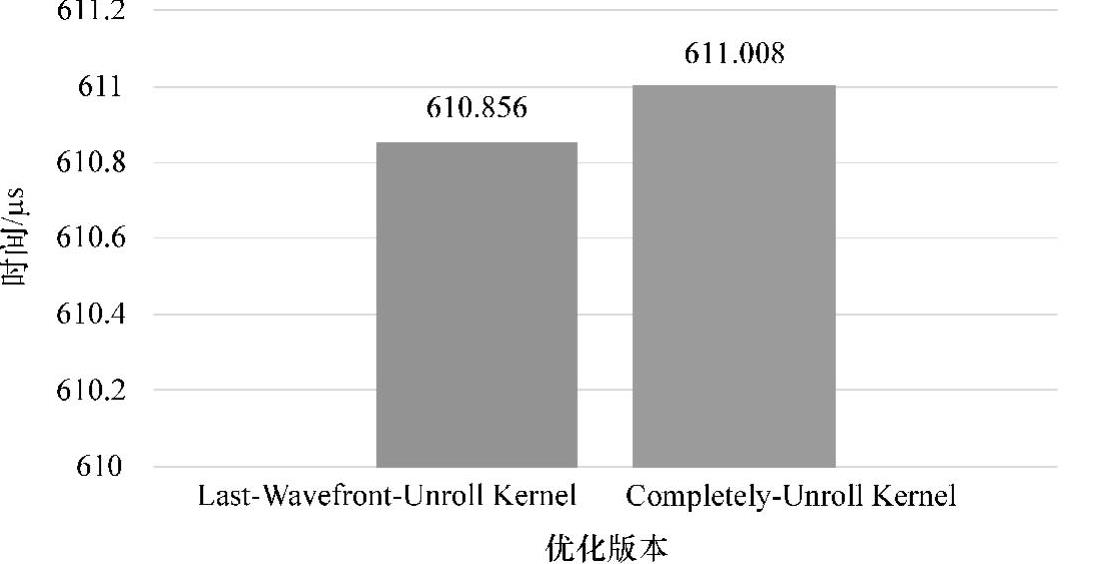
图5-19 循环展开算法

根据5.4.3小节的优化分析，将对线程内规约优化算法的两个版本Stride-Global-Size Kernel与Stride-Local-Size Kernel在两种场景下进行性能的比较，其实验结果如图5-20和图5-21所示。

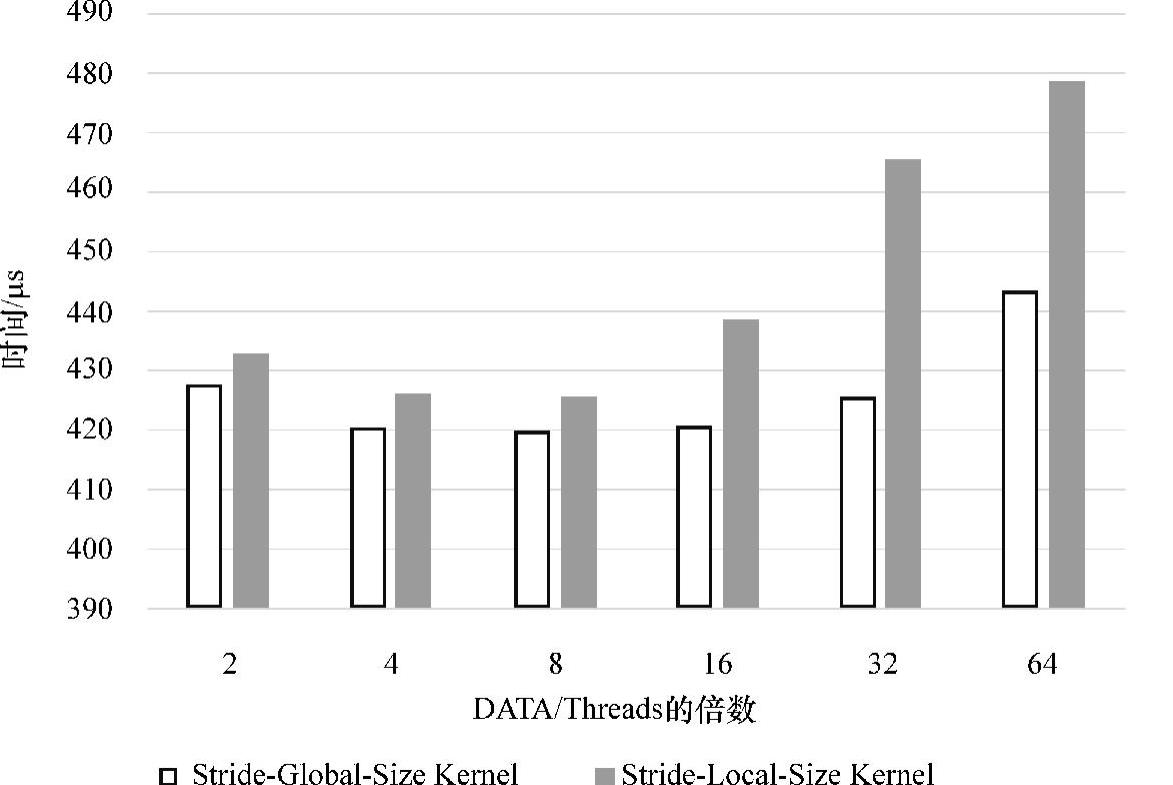
图5-20 场景1：控制全局线程数

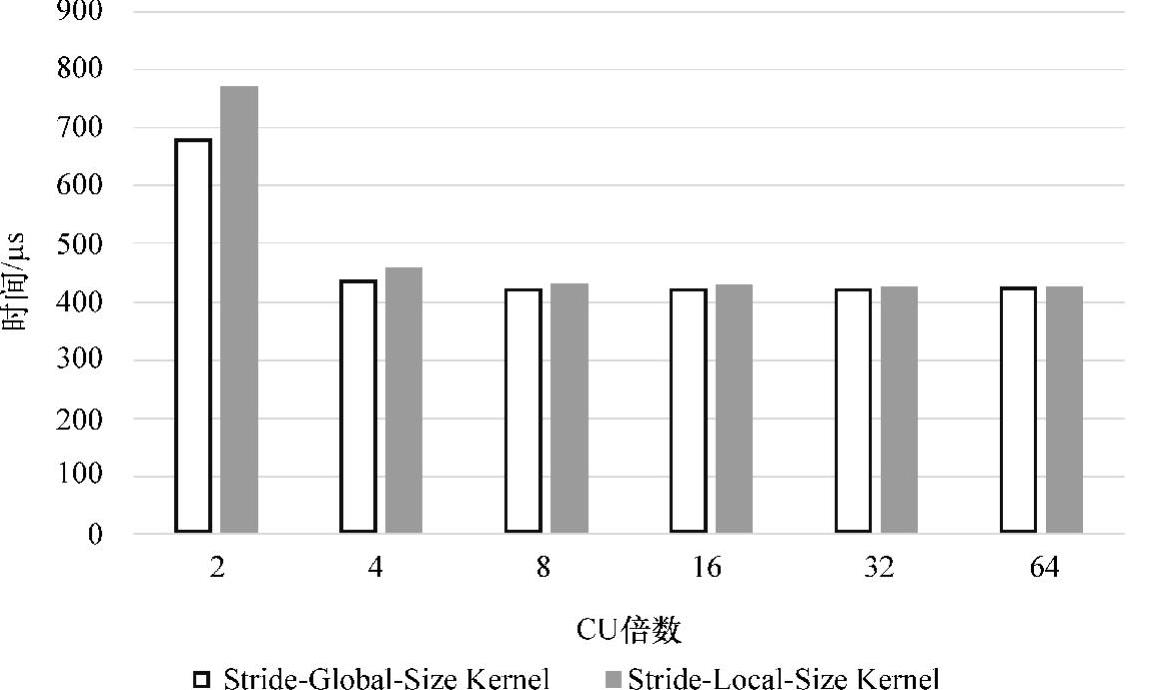
图5-21 场景2：控制work-group数目

两个场景的实验结果同时表明：Stride-Global-Size Kernel和Stride-Local-Size Kernel两个线程内规约算法通过调整倍数参数，其最好性能逼近甚至超过了420μs，相较于图5-19的循环展开算法，性能得到有效的提升。

根据图5-20可知，场景1的work-group数目=全局线程数/局部线程数，全局线程数=数据总数/倍数（图5-20中的2、4、8等），其中局部线程数固定为256。因此，work-group数目随全局线程数波动，数量十分庞大，足以隐藏访问延迟。因此场景1中的两个优化算法性能均能保持在480μs以下。

根据图5-21可知，场景2的work-group数目=CU×倍数，其中AMD Fire-Pro^TMW8000的CU数目为28。可知，当CU倍数参数设置为2，work-group数目为28×2=56时，两个优化算法性能较差，但随着work-group数目的增加，当work-group数目足以隐藏访存延迟时，其性能将会得到提高，如图5-21所示。

然而两个优化算法在场景2与场景1相比较，其work-group数目更均衡地分配至每一个CU，局部和累加的原子操作大量减少，但性能却与场景1相仿。其原因可能是由于work-group数目较少，则在线程内规约优化时单个元素所处理的元素数目增多，从而抵消了原子操作减少带来的性能提升。而由于场景1的work-group数目众多，能有效地隐藏原子操作的访存延迟，因此work-group能否均衡地分配至每一个CU上对性能的影响微乎其微。

由图5-22可以看出，向量化后的性能大约在440μs以内，最优为uint4版本，时间为417.674μs，十分相近，以uint4类型向量效果最优。根据前面的分析可知，GCN架构的GPU对向量化操作的优化十分有限，其对向量化的操作将会拆分成多个标量操作进行。因此向量化优化算法本质上是步长为1的线程内规约算法。

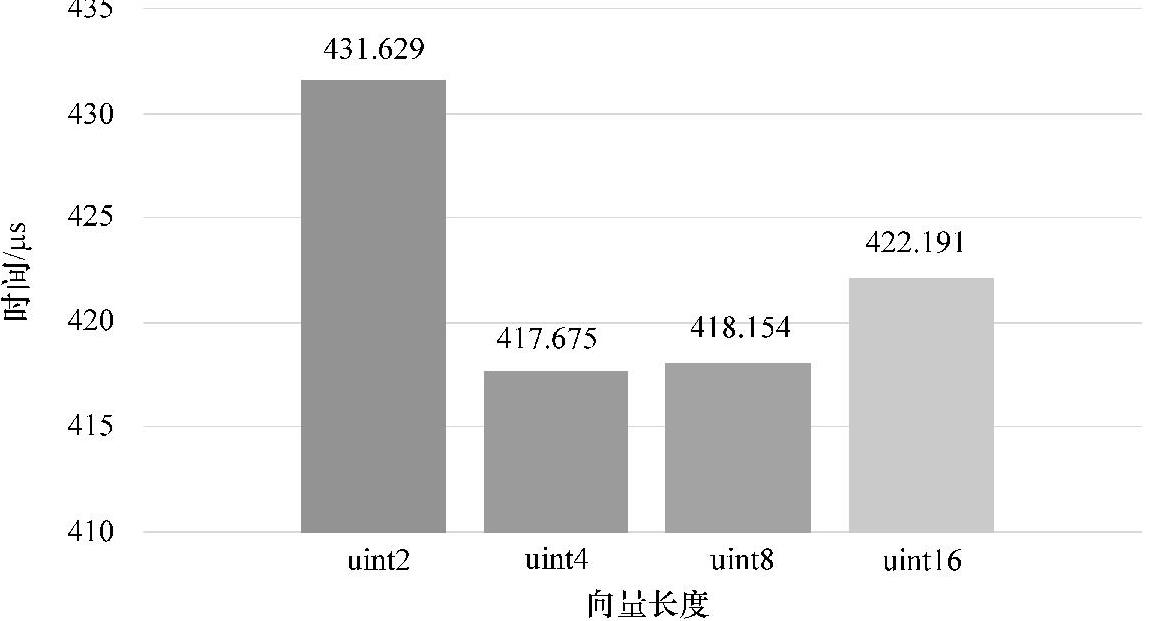
图5-22 向量化优化