从串行规约求和算法Serial Reduce可以看出，每一次的累加需要使用上一次累加的中间结果，以得出下一个循环所需要的中间结果，即每一次的求和运算对上一次求和结果存在依赖。因此，规约算法并不具备并行矩阵转置算法的高度并行性。将规约算法移植至GPU上，首先，要解决迭代间加法计算操作的依赖性，以更大程度地挖掘算法的并行性。本章采用二分规约思想，即一个线程处理两个元素，如图5-15和图5-16所示，每一层规约的完成，规模减半，最后再对合理的、小规模的局部和进行原子累加操作，求出最终总和。此外也鼓励尝试采用四分法、八分法等进行规约。

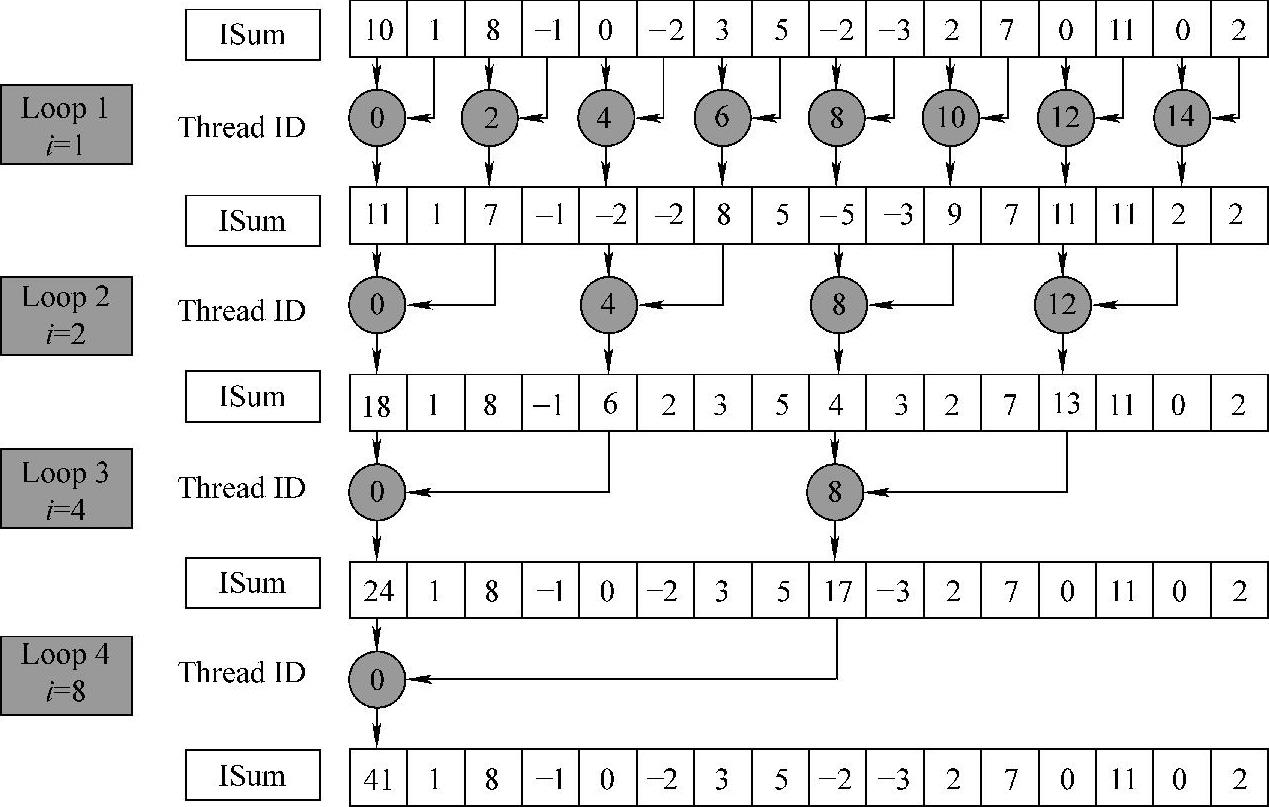
图5-15 Naïve Reduce规约过程

1.并行规约算法简述

根据以上分析，GPU端并行规约算法的过程可以简要描述为三个步骤：

数据传输：work-group把global memory的src数组中对应数据复制至local memory的ISum数组。

work-group内规约：work-group对local memory的ISum数组进行内部规约，求出局部和。

work-group间规约：对每一个work-group所得局部和通过原子操作进行累加，得到最终总和（原子操作atom_add（）作为OpenCL1.2的扩展操作，要包含：#pragma OPENCL EXTENSION cl_khr_global_int32_base_atomics：enable）。

由于规约操作间存在计算依赖，对global memory和local memory的操作又分别涉及合并访问和bank conflict等影响性能因素以及wavefront的编程控制也是影响性能的重要因素，因此衍生出多个版本的并行规约算法。

本章将从基本的并行规约实现开始，针对以上性能因素对算法的三个步骤的并行性进行挖掘，以逐步地提升算法性能，并尝试阐述采用每一步优化方法的依据及思路，以寻求通用的GPU并行规约算法的优化方法。(www.daowen.com)

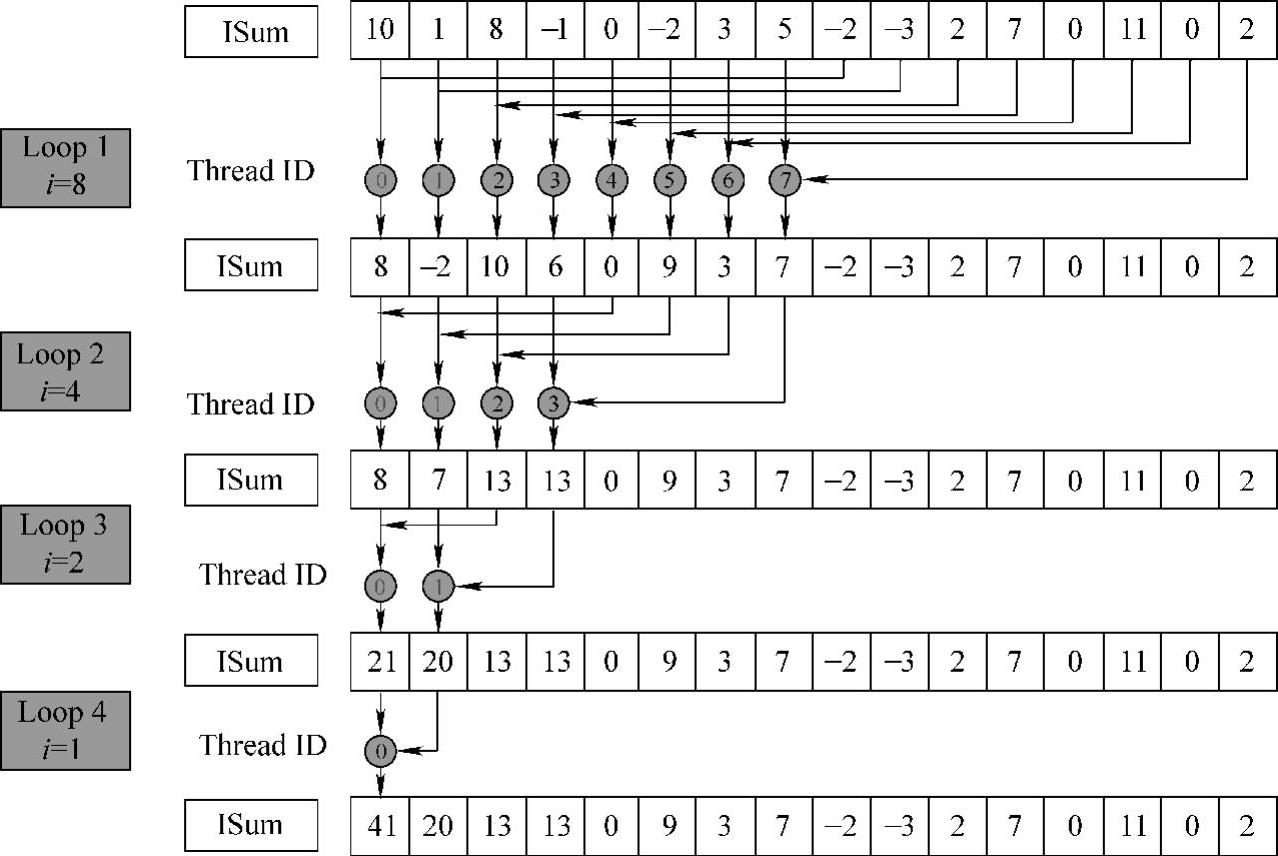
图5-16 Divergence-Free Kernel规约过程

2.并行规约算法基本实现

依据上一部分的分析，采用二分法的Naïve Kernel为并行规约求和算法的基本思路：申请与数据规模等大的线程数目，以使线程和数据一一对应，再根据上一部分的算法三个步骤作为框架进行编码。

数据传输：work-group把global memory中src数组对应的数据加载至local memory的ISum数组，当且仅当work-group内的线程均完成读入操作，对ISum数组的局部规约才能开展。因此，需要显式调用本地同步函数，以确保读入操作完成，即调用barrier（）函数，参数为CLK_LOCAL_MEM_FENCE。

work-group内规约：即局部规约操作，其规约过程如图5-15使用二分法求和，多次循环得出local memory中的局部和。每一次的for循环，需要进行条件判断，通过线程ID以屏蔽部分不需要进行规约操作的线程，此种逻辑判断中，造成相邻的线程无法执行相同工作，从而导致了活跃wavefront数目增加的同时，也导致了wavefront内线程的分支执行，从而影响了程序的并行化，降低了算法性能。

Work-Groups间规约：通过原子累加操作，把每一个work-group规约所得的局部和累加至最终结果位置dest[0]，当所有work-group执行完毕，dest[0]存储最终总和。

其规约过程如图5-15所示。