1.并行矩阵转置算法简述

由矩阵转置算法的定义可知，矩阵转置过程中数据与数据之间不存在依赖，若把线程对原矩阵的读取操作和对转置矩阵写入操作作为元操作，则元操作之间具有高度的独立性，不存在数据依赖。因此矩阵转置过程可以简要描述为三个步骤：

读取原矩阵元素。

计算索引映射。

写入转置矩阵。

通过GPU启动大量的线程，线程之间的操作互不影响，线程取出ID对应的元素，找到索引映射后独立写入转置矩阵位置，由于每个线程所操作的元素各不相同，所进行的索引映射也不相同，最后的结果位置写入操作也不存在冲突，由此可以发现矩阵转置的高度并行性，通过利用GPU众多的计算单元，通过众多线程处理各自的数据单元，线程之间独立执行，实现转置算法的高度并行化。

2.并行矩阵转置算法基本实现

矩阵转置算法在GPU的基本实现极为直观，根据上述的三个步骤，Naïve Transpose可描述为：

读取原矩阵元素：线程通过内建函数获取线程的全局ID，记为x，y，通过x，y结合矩阵的高和宽，即row和col，进而计算线程对应于原矩阵A的元素索引indexIn，并读出该元素A（x，y）。(www.daowen.com)

计算索引映射：通过x，y，row和col，计算线程对应于目标转置矩阵的索引indexOut，（即每一行的索引转换成每一列的索引）。

写入转置矩阵：把元素写入到目标转置矩阵B的indexOut位置，完成B（y，x）=A（x，y），（即A矩阵每一行的元素写入B矩阵的每一列）。

其执行过程如图5-6所示。

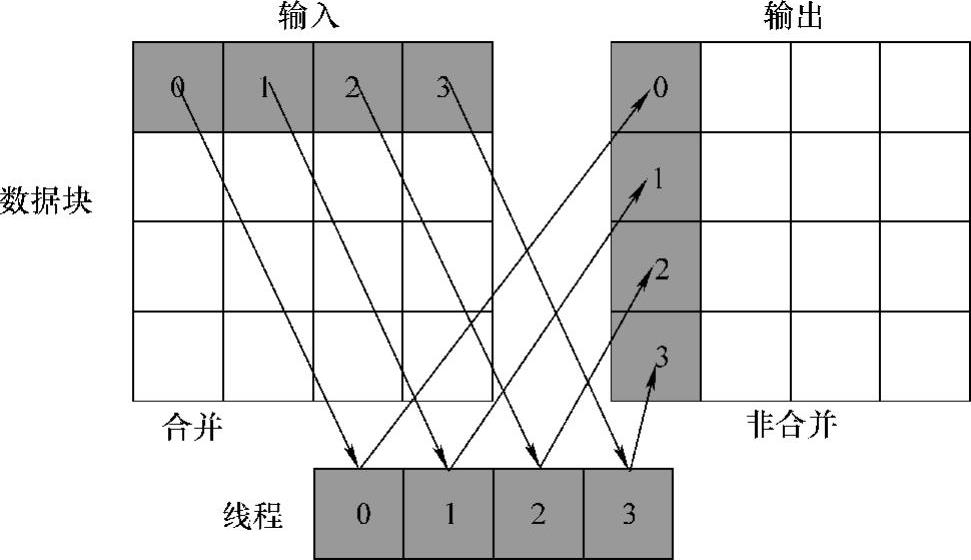
图5-6 Naïve Transpose转置过程

块内的所有线程必须存在于同一个处理器核心中且共享核心有限的存储器资源，所以一个块内的线程数目有限。一个内核可被多个同样大小的线程块执行，所以总的线程等于每个块内的线程数乘以线程块数。线程块可被组织成一维、二维或三维的线程网格。每个执行内核的线程拥有一个独一无二的线程ID，可以通过内置的ThreadIdx变量在内核中访问（块内唯一）。线程块必须独立执行。而且能够以任意顺序，串行或并行执行。这种独立性要求使得线程块可以以任何顺序在任意数目核心上调度。

原矩阵与转置矩阵在转置过程中的数据存放于global memory，从矩阵转置串行算法可以确定出矩阵转置并行算法的基本映射关系，即相同偏移量的线程处理相同偏移量的数据，如图5-6所示。