图3.15给出了在晶体硅太阳电池中电流的路径和方向。电流流向在基体中垂直于底面，但在发射极中平行于发射极方向。细栅线收集来自电池各个区域的电流，主栅线收集各个细栅线的电流。在电流流经的方向存在电阻，电阻会将电能转化成热：

1）背部铝/硅的接触电阻R₁；

2）基体电阻R₂；

3）发射极电阻R₃；

4）前部银电极/硅的接触电阻R₄；

5）细栅线电阻R₅；

6）主栅线电阻R₆。

电阻值正比于导体的长度，反比于导体的横截面积。如图3.15所示，背接触电阻R₁和基体电阻R₂相比于其他电阻要小，这是因为R₁和R₂的横截面积大，基本上是硅片的大小。这可通过一个定量分析进行验证。而其余的四个电阻，发射极电阻R₃、前接触电阻R₄、细栅线电阻R₅和主栅线电阻R₆，往往主导着晶体硅太阳电池中的电阻损耗。而这四个电阻中的三个，即R₃、R₅和R₆，是太阳电池设计中可调的参数。如果可能的话，电池应尽可能地设计成由这三个电阻产生的损耗是大致相同的，这样电池的效率才能最高。

主栅线和细栅线的设计中应该考虑电极带来的遮蔽效应和电阻损失的权衡效果。一旦厚度确定了，细栅线和主栅线的宽度决定了细栅线电阻R₅和主栅线电阻R₆值。宽的栅线有助于降低电阻，但是会遮挡阳光。窄的栅线有助于降低遮蔽损失，但同时会增加电阻损失。通常，我们用来做栅线的金属是银，它在所有的金属中具有最低的电阻率，人们不可能再找到另外一种金属能具有比银更低的电阻率。正如本书第6章中讨论的那样，银在可以预见的未来有可能会被某种地球上高丰度的金属取代，但这些有可能作为电极的金属都比银具有更高的电阻率。

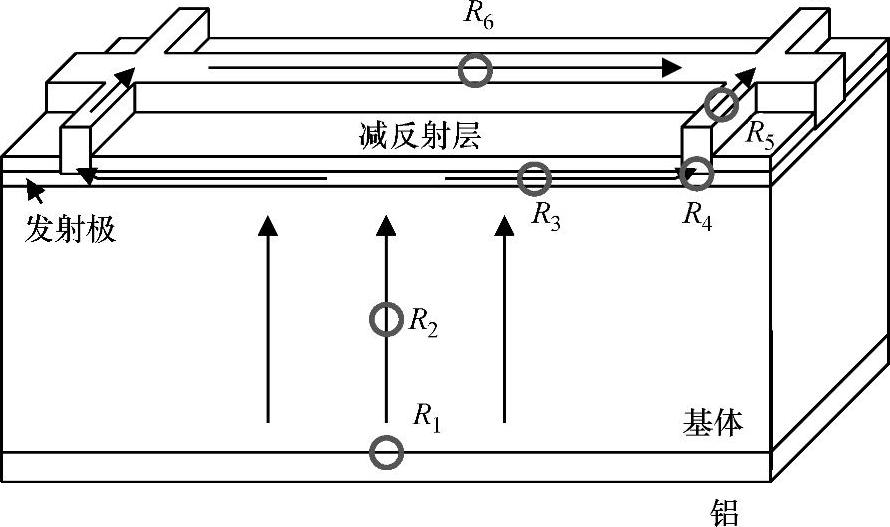
图3.15 晶体硅太阳电池中电流流过的路径与方向。电子流动的方向与电流方向相反。电流流向垂直于底面，但平行于发射极方向。图中，不同的电阻用圆圈标出，包括发射极电阻R₃、前接触电阻R₄、细栅线电阻R₅和主栅线电阻R₆

目前制作金属电极的方法是丝网印刷，其制得的银栅线一般是180μm宽和25μm厚，也就是说高宽比大约是0.3。在电阻损失和遮蔽效应的权衡下一个解决的办法是增加栅线的高宽比，这样会导致相同横截面积下栅线更窄。为实现栅线的高高宽比，丝网印刷的方法已经基本上接近其极限了。另一个解决这一矛盾的办法是降低细栅线和主栅线中的孔隙。晶体硅太阳电池中的银浆料含银纳米颗粒，经过正常的处理后会形成多孔的银层。多孔的银电极层的电阻约为银体电阻的10倍。新的低成本金属化技术例如电镀可以得到致密的银栅线电极。在本书第6章中，我们讨论了可以通过这种电镀的方法制备一些其他的金属电极，如铜或者铝来替代晶体硅中的银。第三个绕开这个矛盾的方法就是将上下电极都做在电池的背面，如上面讨论的背接触电池。(www.daowen.com)

当晶体硅太阳电池被封装成组件时，会将铜线焊接到每个电池单元的主栅线上。这将大大降低主栅线中的电阻损失。因此，细栅线损失变得更为重要。细栅线的有效电阻可表示为^[4]

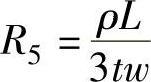
式中，ρ、L、t和w分别是栅线电极的电阻率、长度、厚度和宽度。需要注意的是，细栅线的电阻率ρ并不是等同于而是比银体电阻率高大约10倍。上述公式也可以用来估算主栅线的有效电阻，不过需要假定电流是从电池的边缘收集的，而且没有铜条焊接在主栅线上。

对于图3.1a中的晶体硅太阳电池，n型发射极的掺杂量通常为低的10¹⁹ cm^-3，且发射极的厚度一般为0.5μm。这一掺杂量与p型基体相比高得多，p型基体的掺杂量通常在低的10¹⁶ cm^-3量级。在发射极处也需要对电阻损失和复合损失进行折中。发射极处的高掺杂会大大降低光生载流子的寿命和扩散长度，从而导致高的复合损失。而增加发射极的厚度会导致高复合区域的拓宽，使得复合损失进一步增大。为了降低复合损失，可以通过降低发射极厚度且进行低浓度掺杂来实现。如图3.15所示，降低发射极厚度会减小水平发射极电流的横截面，低的掺杂浓度则会导致发射极电阻的增加。这两方面都会导致发射极的电阻损失增加。对于电池来说，10¹⁹ cm^-3的掺杂浓度和0.5μm的厚度已经是较优的参数了。

在太阳电池设计中的另一个关键参数是细栅线的间距，这同样也需要在遮蔽损失和电阻损失之间进行折中。如图3.15所示，增加细栅线之间的间距会增加发射极处的电阻损失。若减小细栅线之间的间距，会导致电池表面排布了更多的栅线，从而增大了遮蔽损失。如果能开发出一种经济有效的制备细栅线金属电极的方法，适当减小栅线的宽度可以降低遮蔽损失。发射极的有效电阻可表示为^[4]

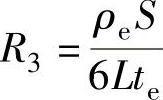
式中，ρ_e和t_e分别是发射极的电阻和厚度；S和L分别是细栅线的间距和长度。

金属和半导体之间的接触电阻主要受两个因素的影响：肖特基势垒高度和掺杂水平。受表面态影响，半导体表面的费米能级通常位于禁带宽度的中部。半导体和任何金属之间的肖特基势垒高度，不论其功函数，大约为带隙的一半。实验测出，n型和p型硅上各种不同的金属的肖特基势垒高度为0.4～0.9eV，而带隙值的一半为0.56eV。因此，目前的太阳电池中的金属/半导体接触实际上是一个具有高的掺杂水平的肖特基结，也就是说，它是一个准欧姆接触。高掺杂水平缩小了肖特基势垒的宽度，使得载流子穿过肖特基势垒发生隧穿效应的概率增加。这样的准欧姆接触的电流-电压关系是线性的。

若金属与一个重掺杂的半导体接触，其以Ω·cm²为单位的比接触电阻可表示为^[5]

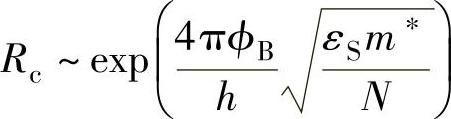
式中，ϕ_B为金属和半导体之间的肖特基势垒高度；ε_S为半导体的介电常数；m*为载流子的有效质量；N为掺杂量；h为普朗克常数。值得注意的是，在一个电池中，发射极的掺杂量通常不是由接触电阻而是由复合损失或电阻损失来确定。因此，通常并不总是通过增加掺杂量来降低接触电阻。另一方面，降低肖特基势垒高度则是一种降低接触电阻的有效方法。这就要求在半导体表面的费米能级不存在钉扎现象，使得肖特基势垒高度能随着金属的功函数的变化而变化^[6]。