根据散粒体颗粒在斜坡上的受力分析，考虑散粒体颗粒在岸坡上的滚动模式，推导出散粒体颗粒在岸坡上的起动流速公式，该公式考虑了河岸坡角、河床纵向底坡以及水流作用力的方向等因素，公式如下［106］：

式中　CD、CL——推力及上举力的系数；

α0、α1、α2——重力、上举力、下滑力对应的面积系数；

γs、γ——泥沙与水的重度；

h、D——水深与散粒体颗粒的粒径；

m——指数流速公式中的指数；

α——底流速作用于床面泥沙颗粒高度的系数；

λ——水流作用力与水平线的夹角；

φ——河流纵向底坡坡角；

g——重力加速度；(www.daowen.com)

θ——河岸坡角，若θ为临界坡，则tanθ＝f（内摩擦角）；

β1——力矩系数；

φ——泥沙颗粒运动方向与下滑力方向的夹角，，。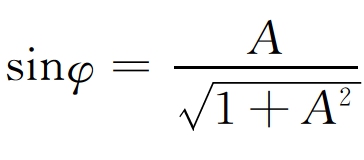

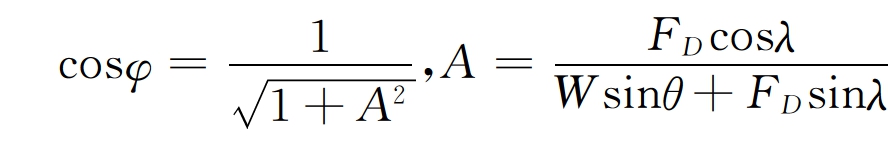就式（8-16）而言，对于粗颗粒泥沙，式中的系数可取为CD＝0.7，CL＝0.18，β1＝0.38，m＝6，α＝1.0。由式（8-16）可看出，散粒体颗粒在不同水流和边界条件下，岸坡上颗粒的起动流速与其大小、岸坡角度、河床纵向底坡等因素有关。例如，起动流速随颗粒粒径的增大而增大，随岸坡的变陡而减小，随河床纵向底坡的增大而减小等。

对于一般性弯道或顺直微弯河道，其横向底流并不大，因此对岸坡上散粒体颗粒的起动流速影响较小。根据公式计算结果比较，在横向底流速为纵向底流速的18％时，其起动流速减小不到0.1m/s，但当横向底流速为纵向底流速的58％时，其起动流速最大减小的幅度超过0.5m/s。在底流与水平方向的夹角为20°时，其起动流速在岸坡越陡处，其减小的幅度越大，最大减小的幅度超过0.5m/s。然而在平坡上底流方向对起动流速的大小没有影响，仅影响其运动方向，这与实际情况是一致的［4］。

表8-7为式（8-16）在不考虑底流方向与横向流速情况下不同粒径散粒体材料的起动流速计算结果。由表8-8 可知，长江中下游河段在平顺护岸工程中，在河岸坡度缓于1∶2、垂线平均流速不大于3m/s的情况下，采用粒径为0.20m左右的散粒体颗粒进行护岸是可以达到稳定的；在河岸坡度缓于1∶2、垂线平均流速不大于2.5m/s的情况下，采用粒径为0.10m左右的小颗粒石料进行护岸也是稳定的，这说明在水流相对较缓的河岸段采用小颗粒石料护岸是可行的。若采用土工合成材料与小颗粒石料如卵石相结合构成排体，则其抗冲性与整体性均得到提高，护岸的效果会更佳，可以考虑用于水流复杂河段的护岸工程。

表8-7　不同岸坡条件下散粒体颗粒的起动流速Uc（m/s）

注　表中的起动流速的条件，水深20.0m，无环流存在φ＝0、λ＝0。

综上所述，在进行护岸工程设计时，须根据护岸河段的平面形态、边界条件、水流条件、河岸组成、工程造价以及对生态与环境影响等多方面因素确定颗粒的粒径与结构型式。