块石自水面落入水中，在水流的作用下经过一段距离沉入河底，自入水点至着底点的纵向水平距离称抛石落距。抛石落距是控制抛石护岸施工质量的重要参数，在求解抛石落距运动的微分方程时，概化的模式是以平均流速均匀分布取代实际流速分布同时考虑惯性力作用的影响，可得块石纵向水平位移X 与下沉时间t 的关系为［81］：

式中　v——平均流速；

α1、α2——分别为块石迎流面积和体积的形状系数；

αx——块石水平运动方向的阻力系数；

D——块石粒径；

ρs、ρ——分别为块石和水的密度。

关于块石沉降速度，经分析，块石在静水中自水面下沉的初速为零作下沉运动时，其沉速ω1与时间t 呈双曲正弦函数的关系为：

式中　αy——块石下沉阻力系数；

g——重力加速度。

块石自水面以上一定距离自由落体，进入水中，若接触水面时的初速ω0大于块石作匀速沉降的速度ω，即ω0＞ω，则块石在水中下沉作减速运动，其沉速ω2与时间t 呈双曲余弦函数的关系为：

上述两条双曲函数曲线将随t 很快趋近ω，

经计算，无论块石在水面投放作加速下沉或按抛石船上离水面一定距离抛石，块石在水中作减速下沉时，约经过0.1s，其沉速值与极限沉速ω 只相差1％～5％。因此，实际上块石下沉中的沉速可近似视为常数ω。引入水深H＝ ωt，得到落距S 基本公式为

说明抛石落距与流速、水深（即单宽流量）、块石粒径、密度、形状及其水平方向和下沉过程的阻力系数有关。显然，S 实际上应为的函数，并能以试验来确定不同尺度与不同形状对块石落距的影响。

为研究块石的抛石落距，长江科学院曾进行了抛石落距试验。在进行试验之前，必须首先确定它的比尺关系。有关研究表明，试验中的块石密度与天然条件下相同，块石形状也相似，在满足水流重力相似条件下，试验中抛石落距的比尺就等于水深的比尺［81］。这就保证了水槽抛石试验成果能应用于抛石设计与施工。

抛石落距试验是在0.6m宽的玻璃水槽中进行。控制水深为15cm、25cm、40cm和50cm，平均流速为0.15m/s、0.3m/s、0.38m/s，组合成不同的单宽流量为0.22L/（s·cm）、0.37L/（s·cm）、0.45L/（s·cm）、0.57L/（s· cm）、0.75L/（s·cm）、0.97L/（s·cm） 和1.53L/（s·cm）。试验块石的形状分别为正方体、扁平体和长方体。试验时，同一颗石子重复投放一般均为400次，每次均测其落距。

试验中观察到块石在下沉过程中，受到水流脉动与抛石入水的姿态等因素影响，每次投抛，块石的运动轨迹是不同的，它的着落点带有随机性。从分析中可知，块石落距的分布是与正态分布有所偏离的，偏离程度随水深、流速和块石特性而异。

通过重复抛投数万次的落距试验，得到关系式为：

式中　k1——考虑各种因素的综合系数；

g——重力加速度；

D——等容粒径。

为了便于实际应用，考虑块石组成中包括各种形状并以重量W 表示的落距公式为：

式中　W——块石重量，以kg计；

v——垂线平均流速，以m/s计；

H——垂线水深，以m计；

S——落距，以m计；

k2——综合影响系数，k2值建议采用0.93。

其余符号同前。

用1966年下荆江中州子裁弯工程冯家潭河段护岸施工时的块石落距试验资料进行验证，表明与上述关系式基本符合［80］。

试验还表明，抛石落距分布的均方差σ值与水深成正比，块石形状对σ值有一定的影响，而块石尺度和流速对σ值的影响似居次要地位。不同尺度、不同形状的块石，在不同流速下σ 的综合平均值与水深H 的关系为：

为了判断抛石量的集中程度，可根据车贝晓夫不等式来考虑［81］。当ε＝3σ，即抛石在平均值s ±3σ范围内的数量不小于89％。越接近正态分布，在该范围内的数量越多。

在抛石施工中，可以根据s值做到恰当的定位，在进行水下抛石修建潜坝时，根据σ值可了解块石分布范围。在平顺抛石护岸施工时，在不同水深下抛石船纵向移位的距离可按约90％ 的石量将落在±3σ（即6σ） 范围内来确定。这样可以做到抛石比较均匀，同时又有一个合理的移位距离。目前，长江中下游通常采用的10m×10m的抛石网格进行定量投抛和相应的船只移位，对于近岸10m左右水深基本上是可以保证质量的。对于大于10m水深的离岸较远的河床，其均匀程度将会更高，实际上完全可以按照σ值以较大的施工方格，以减小定位船移位次数，从而提高功效。(www.daowen.com)

2005年，长江科学院又进一步开展了抛石落距试验[5]。结合以往的抛石落距试验资料分析，对于不同形状的块石，k1和k2值有一定差别（表8-3）。由表可以看出，在同样水流条件下，球体的落距最小，立方体的次之，而长方体与扁平体块石的落距相差较小，落距最远，主要原因是由于不同形状的物体在下沉过程中受水流的阻力不同，球体在下沉过程中受的阻力明显小于其他形状体。根据不同形状的块石落距资料综合分析，得到影响抛石落距的系数k1＝ 1.078，k2＝0.90。另外，试验过程中发现块石落距与其入水时的姿态也有一定关系。

表8-3　k1、k2值与块石形状关系表

为了比较试验公式计算值与原型实测落距值的差别，将二者点绘成图（图8-7），从图8-7可看出，原型抛石落距主要集中在公式线的两边，与试验观测是一致的，但扁平状与长方体的块石偏离较大，且落距明显大于立方体与球体。根据试验成果分析以及原型落距实测资料进行对比分析可知，在抛石护岸工程设计中，抛石落距的综合影响系数可按k1＝1.078，k2＝0.90来考虑。但在施工过程中，由于河道的水流条件及块石的形状等都比较复杂，根据现场试验可适当调整k2的值，以与实际情况一致。

图8-7　试验公式与长江护岸抛石落距实测资料比较图

为了表明抛石落距既有一定的规律性，又呈现出一定的随机性，进行了定点投抛试验，投抛的碎石每次在500颗左右，其粒径为0.65～0.85cm，垂线平均流速0.15～0.52m/s，水深0.29～0.51m，结果发现这些碎石在水下形成一定长度与宽度的离散抛石体，且垂线平均流速与水深越大，形成的抛石体就越长，宽度也越大，但抛石体宽度的变化幅度小于长度的变化幅度（表8-4）。试验中还观察到在水浅流速较小的情况下，易形成石堆，如流速小于0.08m/s，投抛到水下的碎石集中成堆，主要原因是在低流速情况下，水流的脉动强度和纵向流速相对较小，因此，抛投到水下的碎石被限制在更小的范围内，易成堆。以上试验结果表明，在水深流速大的位置，只要按设计要求施工，抛石分布可达到相对均匀；在水浅流速小的位置，则可能会出现石堆与石埂现象。因此，在水浅流速小的位置施工要更加注意施工质量，以便块石在岸坡上尽可能均匀分布。

表8-4　块石定点投抛试验成果表

詹义正对球体在动水中的移距和稳定移距进行了较深入研究［82］，认为球体一方面受重力作用沿Y（水深）方向下沉；另一方面受水流的挟带推移作用沿X（纵向水流）方向作水平位移。通过试验观察到球体在动水中的运动轨迹呈平滑的下凹曲线，由于流速分布沿水深变化导致推移球体运动的力在不断改变，因此球体在接近槽底前有急促下沉的现象，尤以比重较大的球体更为明显。并在流速沿垂线分布服从指数流速分布规律的条件下，推导获得了球体在动水中的运动轨迹方程：

及落距计算式：

式中　；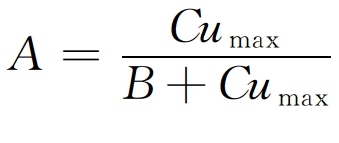

ω——球体的静水沉速；

H——水深；

ρs、ρ——球体及水体密度；

d——球体的直径；

M、N——待定参数，按球体静水沉降曲线资料可以近似确定为M＝24，N＝0.45；

U——垂线平均流速；

umax——垂线最大流速；

υ——水的黏滞系数。

利用试验资料和原型观测资料对上述公式进行验证表明，公式结构合理，计算结果与观测资料符合较好（图8-8、图8-9）。

图8-8　方程（8-13）与实测资料对比图

詹义正还认为，沉落于河底的球体，一方面受当地水流的推移作用，另一方面还受到前期运动的惯性作用影响，因而与床面接触后的球体，有时可能具有一定的初速度us0。在这种情况下，球体主要受3个力的作用，即促使球体运动的水流作用F1、球体做变加速运动的惯性力F2（包括上举力）以及阻止球体沿床面运动的摩擦力F3（图8-10）。降落于床面后的球体能否再度运动，主要受制于这几种力的综合作用结果，据此得到了相应的稳定移距公式［96］。

图8-9　方程（8-14）与实测落距相关图

（a）球体落距；（b）非球体落距

图8-10　球体受力分析图

此外，1964年杨国炜[6]在研究动水中沉降问题中，认为球体在动水中的绕流图案可视为其在静水中因重力作用发生沉降（Y 方向，自水面起）所引起的绕流与其因动水推移作用发生位移（X 方向） 所引起的绕流之组合。它改变了相应于静水情况下的绕流流线，使尾涡发生偏转。阻力R 相对于重力方向产生偏转角α1，以及形成侧面力f。由此可写出X 方向上的力学平衡方程为：

式中　M′——球的质量；

us——球在X 方向上的运动速度。

方程（8-15）所考虑的因素是较为全面的。偏转角α1的大小反映了球体在动水作用下的转动，阻力R 在Y 方向上的投影反映出动水对沉降速度的影响；在X 方向的投影反映了动水对球体的推移（或阻碍） 作用的情况，但是要求解该方程在数学上是十分困难的。

1978年，梁润在研究河道截流工程中的抛石稳定落距等问题时，将实际流速分布概化成垂线平均流速。由此解X 方向上的运动方程，可获得块石在动水中的运动规律及落距Xd的表达式［83］。

对于块石在静水中的沉降机理和沉降速度，毛世民等人于1964年进行了室内试验，并提出了块石在静水中的沉降公式[7]。