实验分别比较了如下6种BP算法训练得到的ANN BP的训练过程及结果：

1）有动量的梯度下降法（对应ANN工具箱函数：traindm）；

2）有自适应lr的梯度下降法（对应ANN工具箱函数：traingda）；

3）能复位的BP训练法（对应ANN工具箱函数：trainrp）；

4）量化共轭梯度法（对应ANN工具箱：trainscg）；

5）一步正割的BP训练法（对应ANN工具箱：trainnoss）；

6）Levenberg-Marquardt训练法（对应神经网络工具箱：trainlm）。

在每个训练方法的训练过程中，均保留了较好的（网络）分析结果图。以下是各算法的训练结果。

图3-8所示为动量的梯度下降法的训练过程及分析结果图。

图3-9所示为自适应lr的梯度下降法的训练过程及分析结果图。

图3-10所示为能复位的BP训练法的训练过程及分析结果图。

图3-11所示为量化共轭梯度法的训练过程及分析结果图。

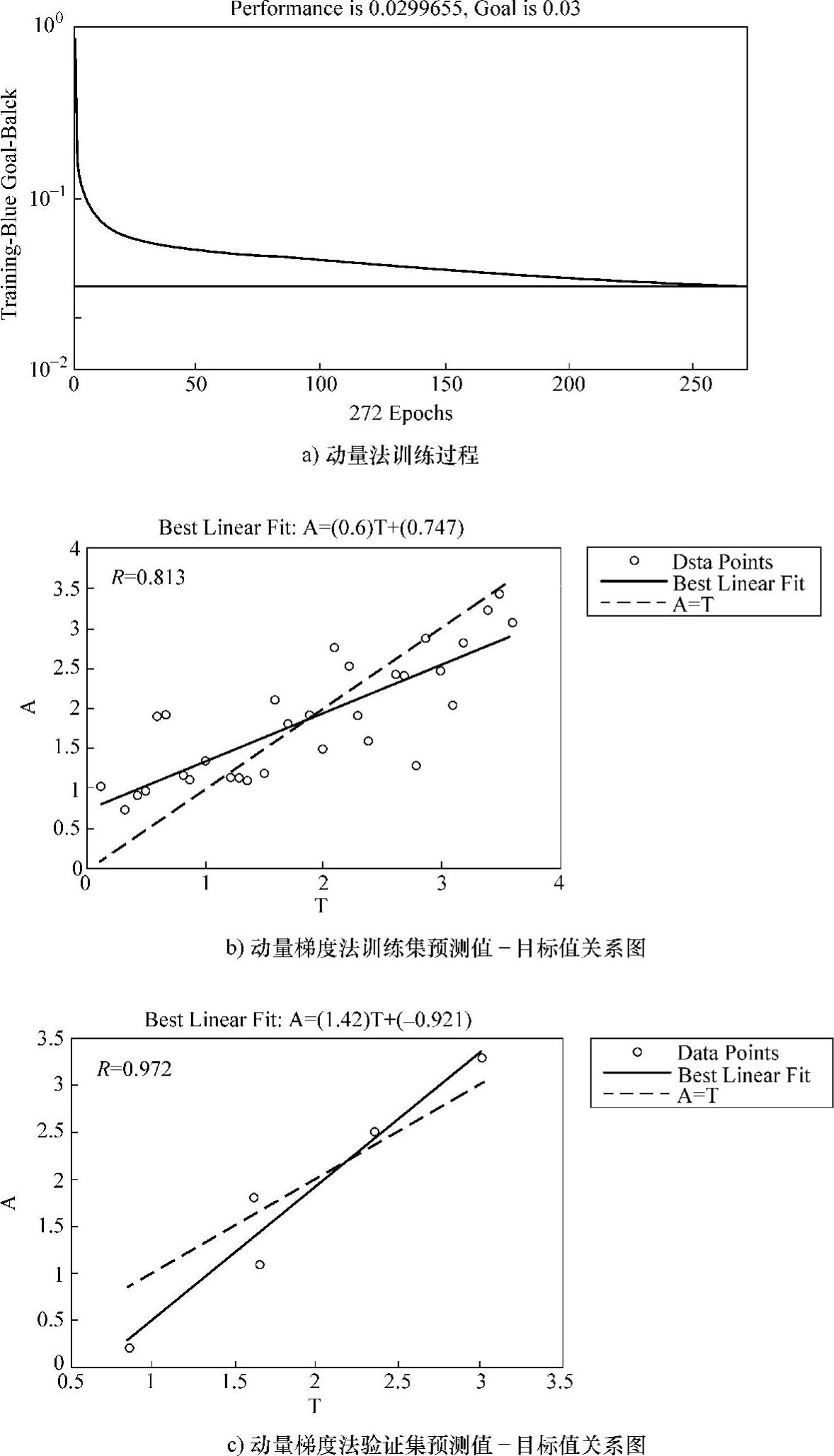
图3-8 动量的梯度下降法的训练过程及分析结果图

图3-12所示为一步正割的BP训练法的训练过程及分析结果图。

图3-13所示为Levenberg-Marquardt训练法的训练过程及分析结果图。(www.daowen.com)

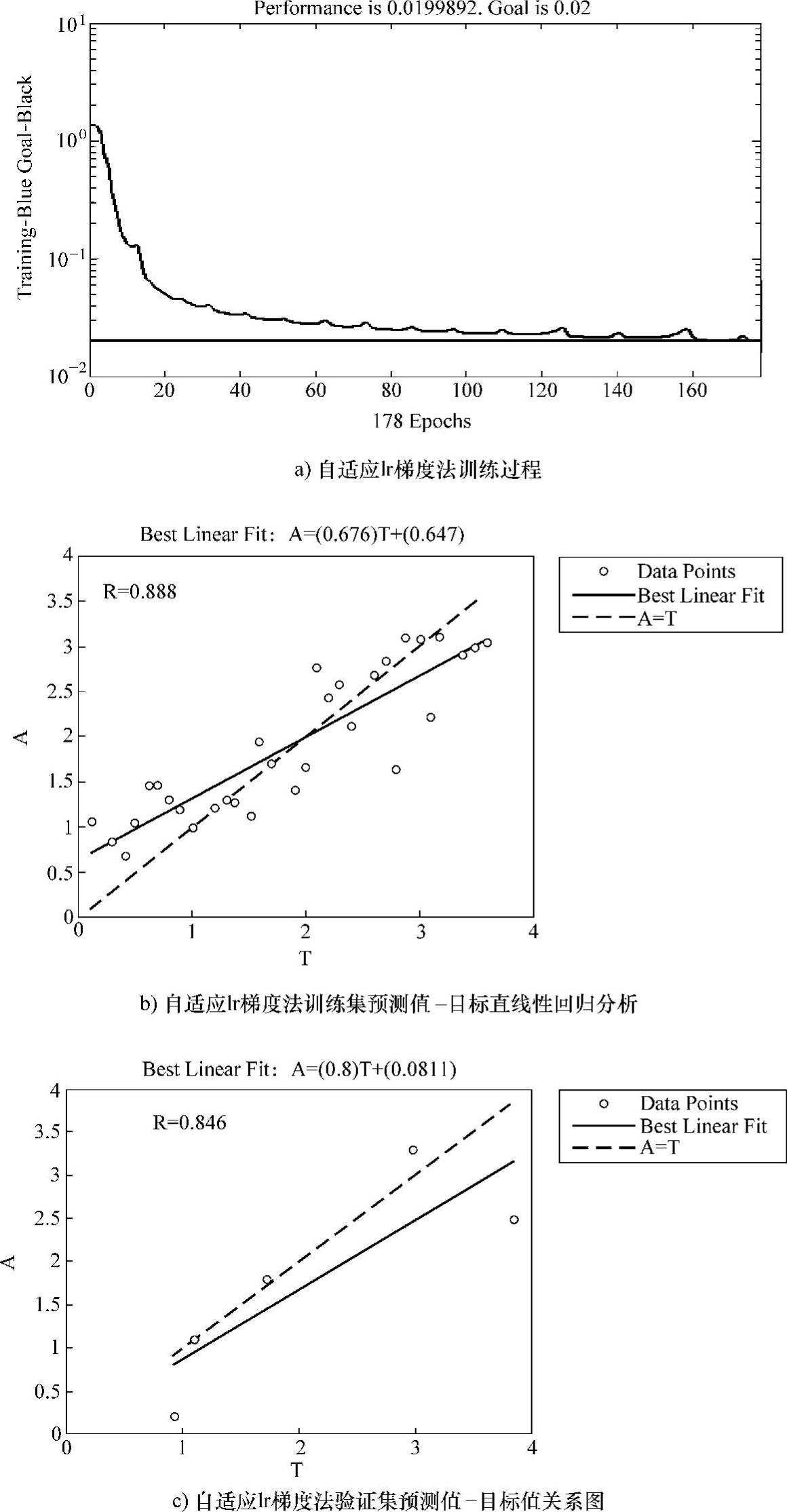
图3-9 自适应lr的梯度下降法的训练过程及分析结果图

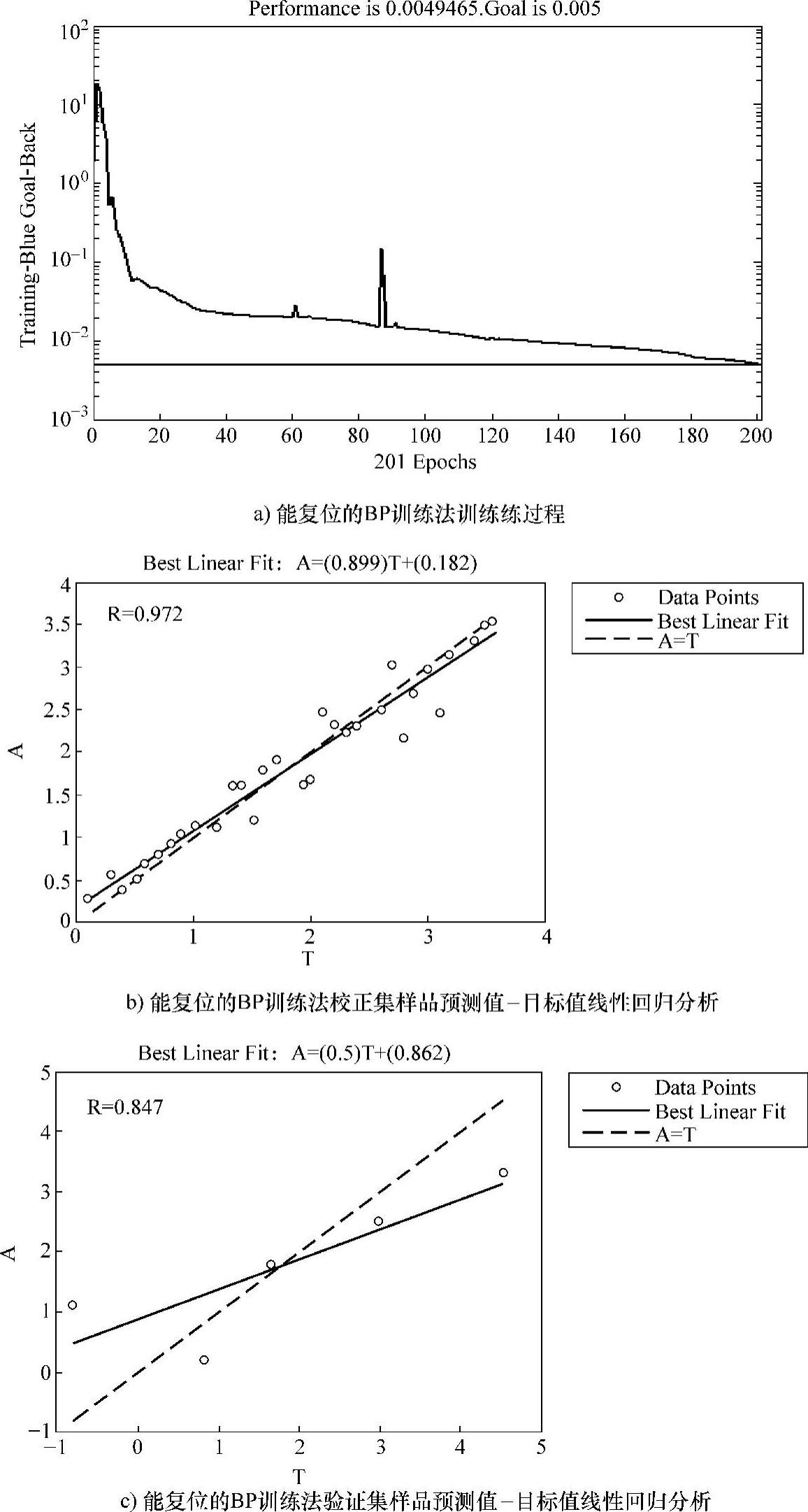
图3-10 能复位的BP训练法的训练过程及分析结果图

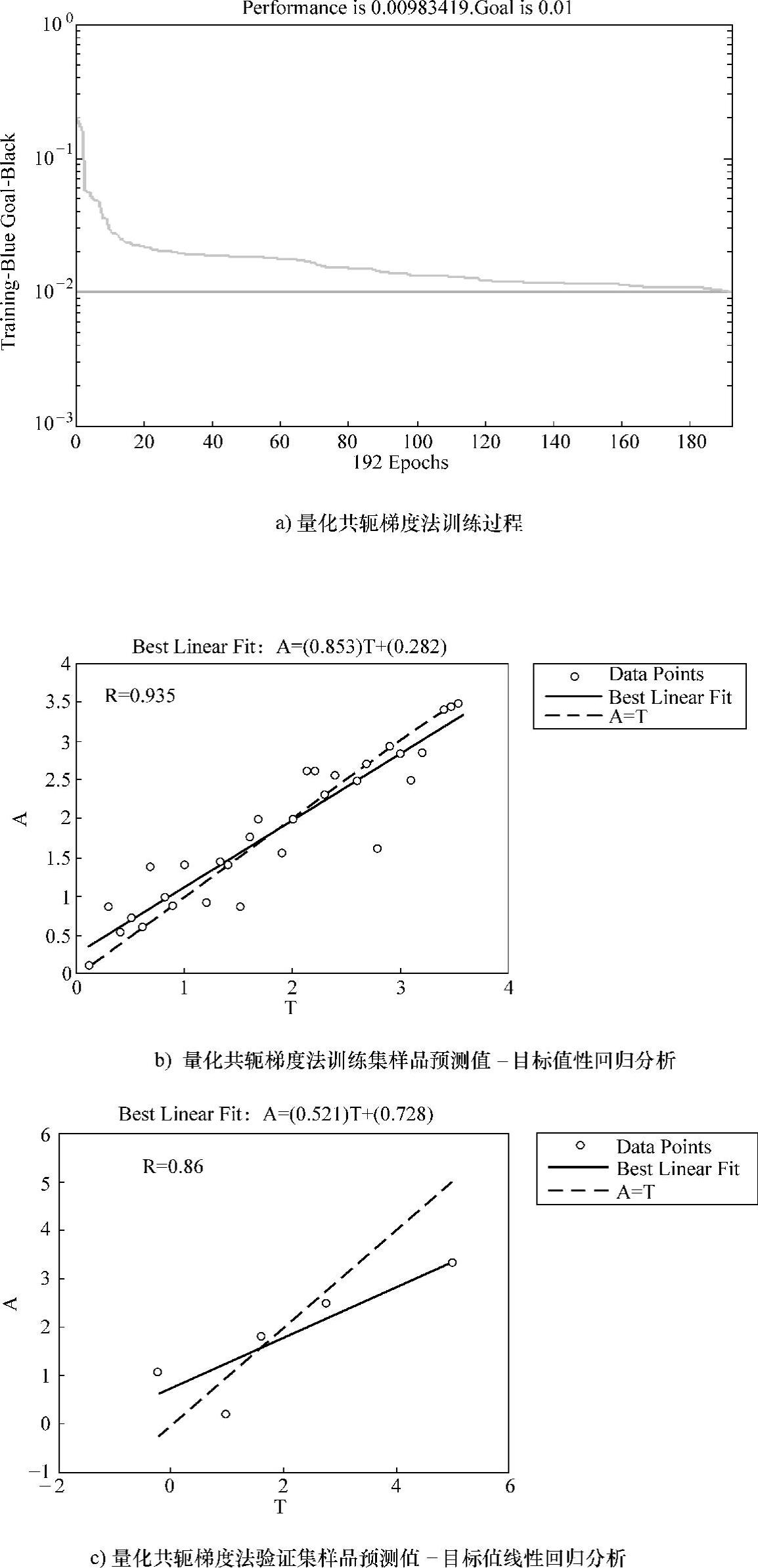
图3-11 量化共轭梯度法的训练过程及分析结果图

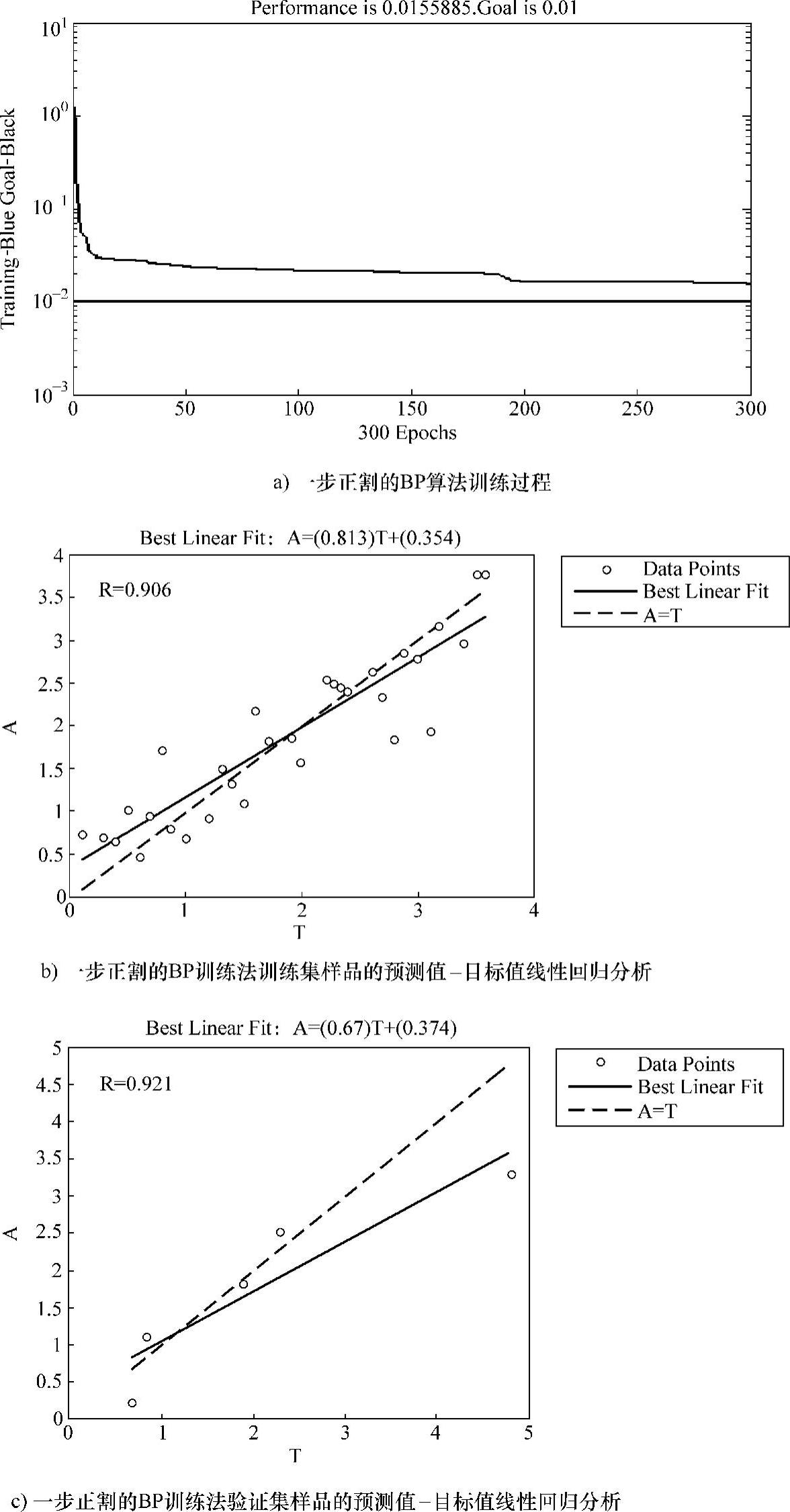
图3-12 一步正割的BP训练法的训练过程及分析结果图

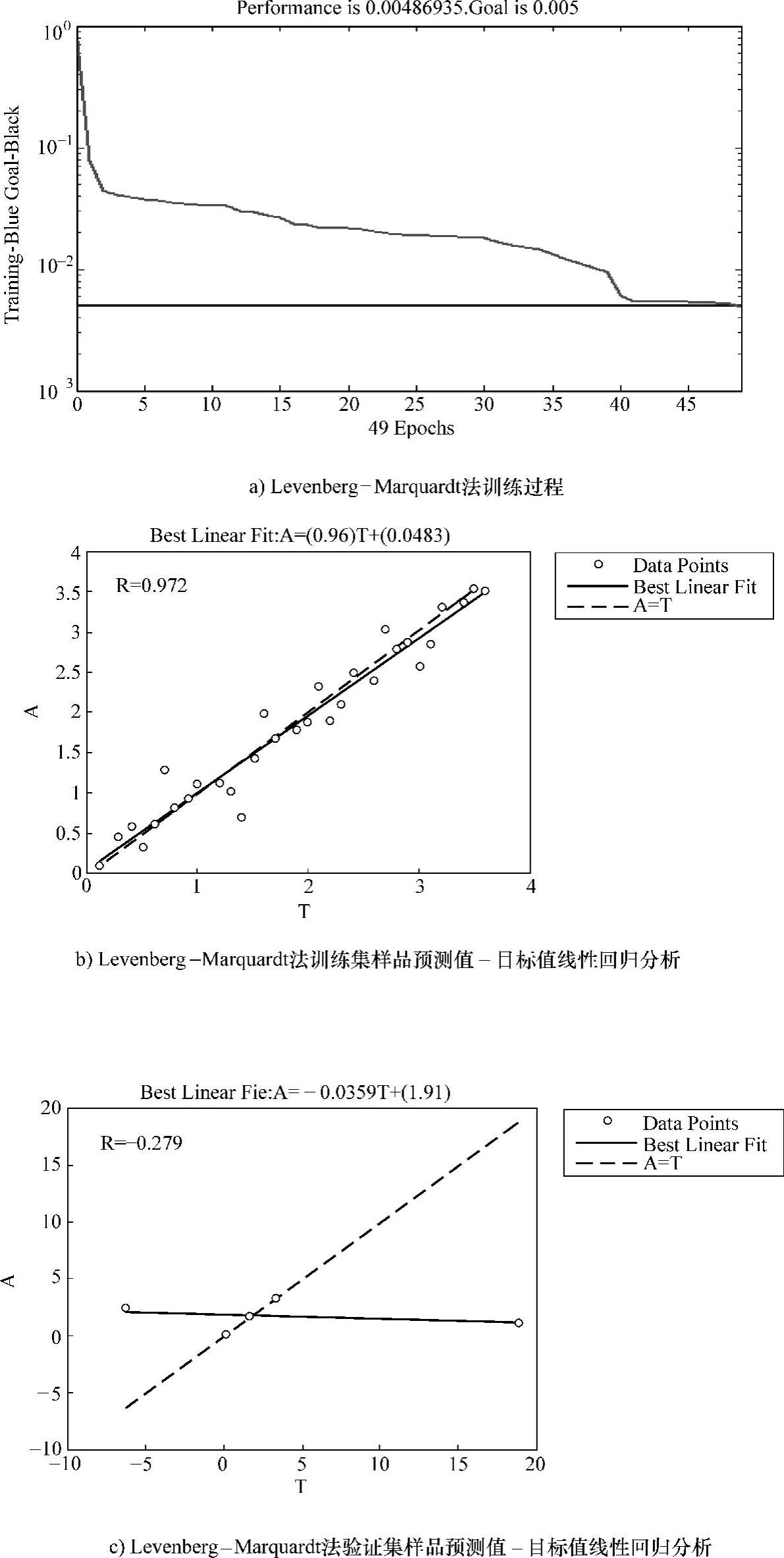
图3-13 Levenberg-Marquardt训练法的训练过程及分析结果图

6种算法下训练得到的ANN BP见表3-5。

表3-56 种算法下训练得到的ANN BP

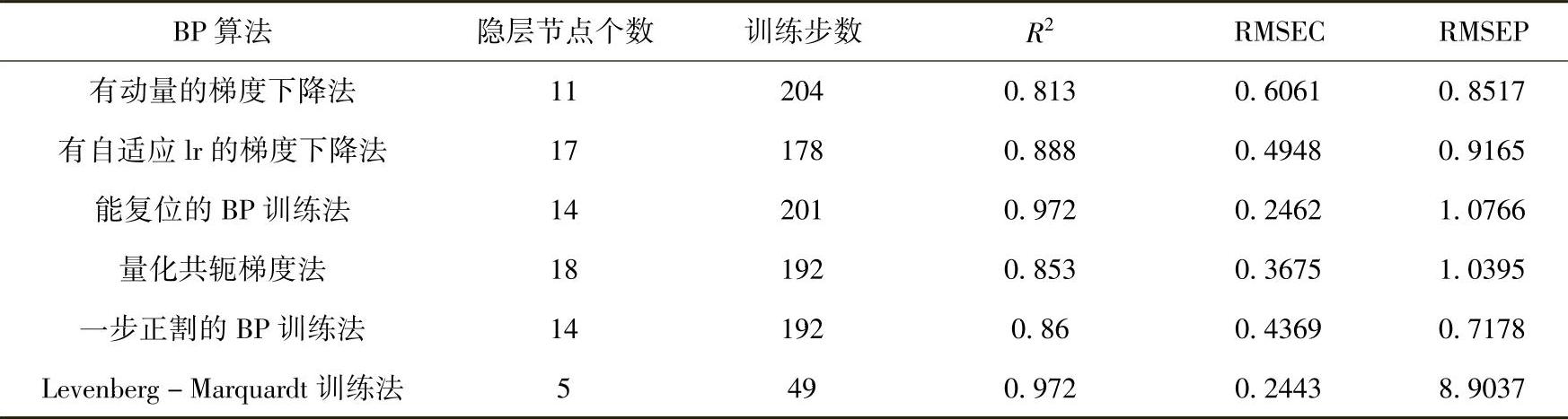
前5种算法在一定程度上均提高网络的训练速度，且模型的自预测能力较高。尤其是一步正割的BP训练法训练速度最快，模型最稳定。Levenberg-Marquardt训练法占用内存空间大，收敛很慢，因此训练过程时间长。如果内存有限，可以采用其他收敛速度较快的算法。对于大型网络，就要采用其他训练函数，例如trainscg或者trainrp。

基于经验风险最小化原则的神经网络学习过程中过分强调得到较小的训练误差，导致泛化能力的下降，因此训练得到的ANN BP对验证集样品的预测能力差。