支持向量机（SVM）是一种机器学习的方法，其基础上统计学习理论，基本思想是在样品空间或特征空间中，构造一个最优决策的超平面，使得该超平面到不同类样品集之间的距离最大，从而使算法的泛化能力得到提高。该方法是一个凸二次优化问题，能够得到全局最优解。此外，SVM较传统的神经网络具有收敛速度快、容易训练、不需要预设网络结构等优点。因此SVM在模式识别、数据挖掘、函数逼近、图像处理方面都得到了广泛的应用。

SVM是由Vapnik等人1998年在统计学习（Statistic Learn Theory，SLT）的VC（Vapnik-Chervonenkis）维理论和结构风险最小原理基础上提出的一种方法，根据有限的样品信息在模型的复杂性和学习能力之间来寻求最佳折衷，以期获得最好的推广能力。用小麦粉的水分、灰分及面筋与仪器响应之间并非简单的线性关系，而是由近红外光谱的吸收特性提供的物质的物理状态信息得到的值，SVM可以通过非线性核函数，将输入样品空间映射到高维线性特征空间，可以处理高度非线性回归等问题。应用SVM进行回归可减少训练时间、避免陷入局部极小，提高了模型的学习泛化能力。

SVM算法原理如下：

1）将原始样品数据进行相应的预处理有利于加快模型的样品训练速度和收敛速度，提高预测精度。这里采用归一化处理方法：

式中，x_（i）为归一化后的数据序列值；x_max、x_min分别为数据样品的最大值和最小值。

2）假定输入样品集为n维矢量，样品及相应输出值可以表示为（x₁，y₁），…，（x_k，y_k）∈R_n×R，函数回归就是用训练样品进行训练得到一个函数式f（x）=（w·x）+b，使训练样品外的x集合能够通过f（x）映射到对应的y集合。

3）设从样品空间到高维特征空间的映射函数为φ（x），则求解函数f（x）参数的问题就

转化为在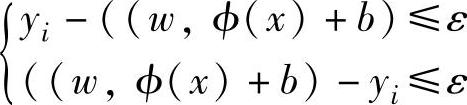i=1，2…，l约束条件下求函数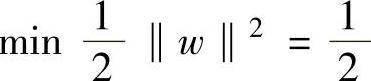（w·w）的最小值的优化问题。

4）一般特征空间的维数很高而且目标函数不可微，所以求解上述的SVM回归问题一般都通过建立拉格朗日函数，将上述问题转化为在式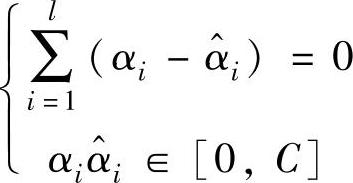，约束下求解式

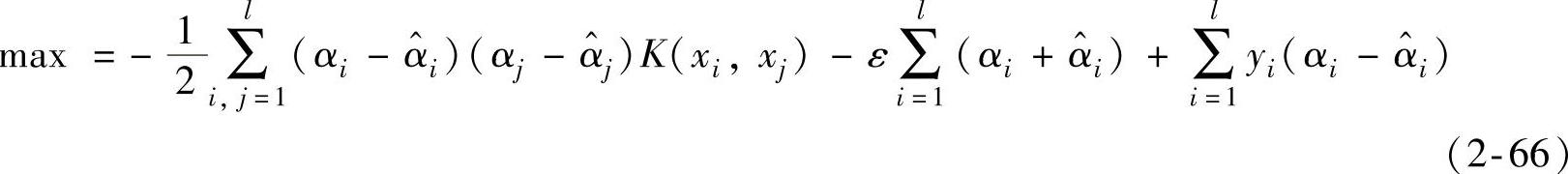(www.daowen.com)

式中，α_i和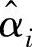为拉格朗日乘子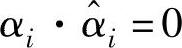，，αi和。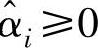

在求解二次优化的问题时所得到的拉格朗日乘子，α_i和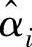中只有一小部分不为零，支持矢量即拉格朗日乘子所对应的数据点。

5）这样SVM回归的问题就转化成为一个二次规划问题，SVM回归的函数就是由这些支持矢量决定。求解后得到回归函数式：

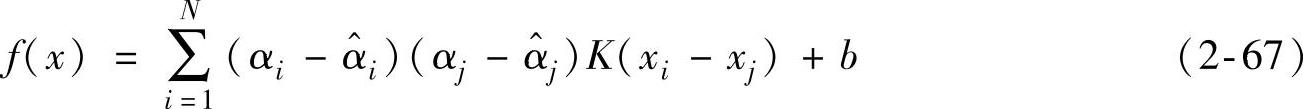
式中，矢量x_i和x_j分别为在特征空间ϕ（x_i）和ϕ（x_j）中的内积，K（x_i-x_j）即核函数，N为支持矢量的个数。

SVM的算法流程如图2-8所示。

图2-8 SVM的算法流程

为了减少运算量，提高运算速度，采用主成分分析法对原始的近红外光谱矩阵进行降维，取累计贡献率达到99.5%的特征矢量为SVM模型输入的特征子集。惩罚系数c、不敏感系数g、核函数及相关参数的选择，对SVM的效果有显著的影响。K-CV（K-fold Cross Validation）是把原始的数据分为K组，将每个自己作为一个验证集，同时K-1组自己作为训练集，得到K个模型，用这K个模型最终验证集的准确率的平均数作为K-CV的性能指标，K-CV可以有效地避免过学习和欠学习状态的发生，使用K-CV选择参数使SVM模型得到较好的预测结果；CV是在没有先验知识指导的情况下一般选用径向基函数（RBF）为核函数，RBF可以将非线性的样品数据映射到高维特征空间，降低模型的复杂性，提高训练速度。这里SVM模型参数的选取RBF为核函数，并采用交叉验证算法来确定相关参数。