模式识别方法是20世纪50年代早期提出的，60～80年代在各个学科得到广泛应用。到80年代，模式识别方法发展成为一种非常成熟的多元分析方法。

模式识别方法可分为有管理方法、无管理方法和显示方法等几类。有管理模式识别包括线性判别、逐步判别分析、KNN方法、SIMCA方法、神经网络等；无管理方法包括最小生成树、聚类分析等；显示方法包括变量-变量绘图、线性投影、非线性映射、脸谱法等。

在模式识别中是根据“物以类聚”的原则进行样品分类的，即性质或特征或变量相似的样品聚为一类。化学模式识别中常用相似系数（similarity coefficient）表示相似性。相似系数表示方法有许多形式，而“距离”（distance）便是相似性[或相异性（dissimilarity）]的量度。

设样品x_i和x_j（测量数据矩阵X中的两个行矢量）之间的距离为D（x_i，x_j），作为距离必须满足以下条件：

1）当x_i=x_j时，D（x_i，x_j）=0，即同一个样品距离为零；

2）x_i≠x_j时，D（x_i，x_j）＞0，即不同样品距离大于零；

3）D（x_i，x_j）=D（x_j，x_i），即距离没有方向性；

4）D（x_i，x_j）≤D（x_j，x_i）+D（x_k，x_j），即两点间直线距离最短，这里下角k表示第3个样品。

化学模式识别中常用的距离指标较多，比较主要的如下：

1.欧氏距离（Euclideandistance）

式中，p为变量数，如写成矢量形式有

在某些场合，对于不同的变量需给予不同的权重，则有加权欧氏距离（weightedEuclid- eandistance）：

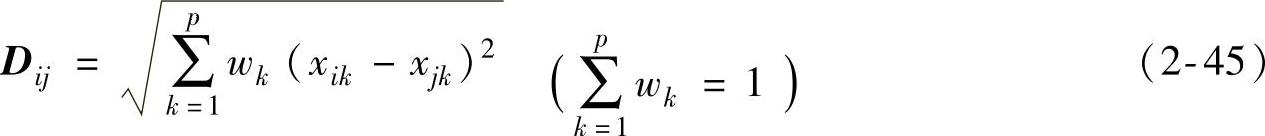
标准欧氏距离（standardEuclideandistance）为

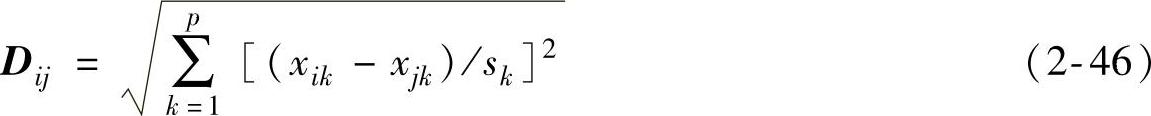
式中，s_k表示测量数据矩阵X中第k列的标准偏差：

实际上标准欧氏距离是预先将测量数据矩阵X标准化后所确定的矢量间的距离。

2.马氏距离（Mahalanobis distance）

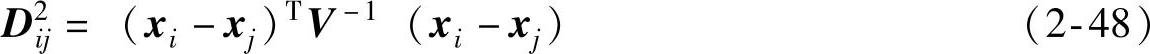
式中，V为协方差矩阵，其元素v_lm为

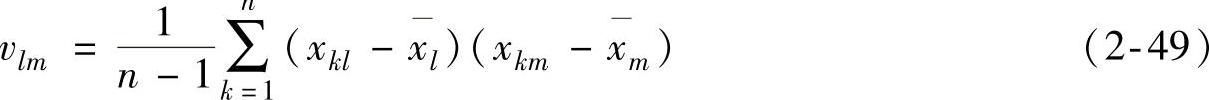
马氏距离实际上可以看作一组样品的中心与某一目标之间的距离，该距离考虑了样品与样品之间的相关性。欧氏距离相等并不表示马氏距离也相等。

在样品很多的情况下，对预测样品进行模式识别时，人们通常事先并不知道样品内在的分类。其中无监督模式识别方法在未知训练集样品的类别的情况下，同样可以对样品进行分类识别。聚类分析法便是无监督模式识别法的代表。

常见的聚类分析方法有系统聚类法、最小生成树法、最短生成路径法和判别聚类的势函数法等。其中系统聚类法是在近红外光谱分析中应用较为广泛的一类聚类分析方法，其基本思想是首先定义样品之间和类与类之间的距离。在各自成类样品中，将距离最近的两类合并，重新计算新类与其他类之间的距离，并按最小距离归类，重复此过程，每次减少一类，直到所有的样品成为一类为止。其聚类过程用图表示，称为聚类图，如图2-6所示。

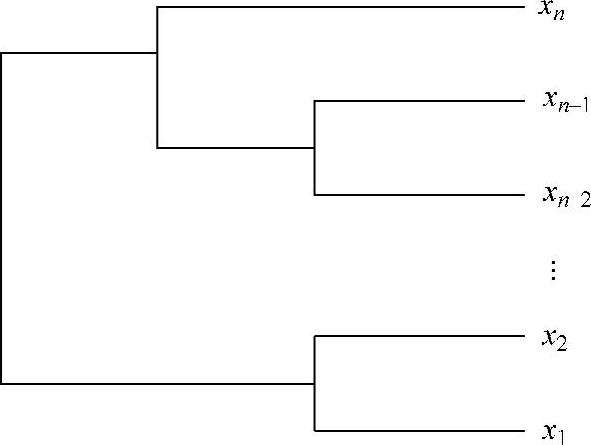
图2-6 系统聚类图

类与类间的距离又有不同的定义方法，因此产生了系统聚类的不同方法，而常用的有8种方法：最短距离法、最长距离法、中间距离法、重心法、类平均法、可变类平均法、可变法和离差平方和法。下面分别介绍这些方法。

（1）最短距离法

设G₁，G₂，…，G_n表示n类，d_kl表示样品k、l间的距离，D_ij表示类G_i、G_j间的距离，则

最短距离法的聚类步骤如下：

1）计算所有样品间的距离，得距离矩阵D_（0），各样品自成一类，此时D_ij=d_ij。

2）在D_（0）非对角线元素中选取最小元素，设为D_ij，将G_i与G_j合并为一类，记作G_r，则{G_i，G_j}即G_r中的样品，为G_i、G_j中的全部样品。

3）计算新类G_r与其他类G_s间的距离D_rs。

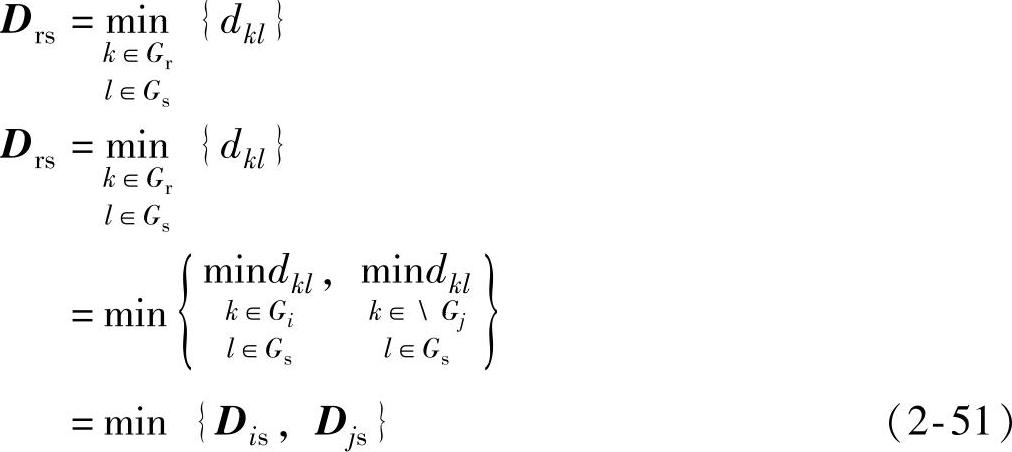
由此得到距离矩阵D_（1）。

4）对D_（1）重复D_（0）的步骤得D_（2），如此继续下去直到所有样品都归为一类为止。

（2）最长距离法

最长距离法规定两类间的距离为两类中最远样品间的距离，即(www.daowen.com)

同最短距离法步骤一样，只是在两类G_i、G_j合并为新类G_r时，G_r与其他类G_s间距离为

（3）中间距离法

中间距离法定义类间距离采用介于最短距离与最长距离法之间的距离。设某一步将G_i与G_j合并为G_r，则G_r与其他类G_s间的距离定义为

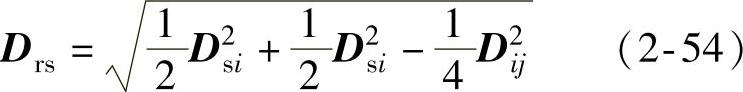
几何意义如图2-7所示。

中间距离法可推广到更一般的形式，即

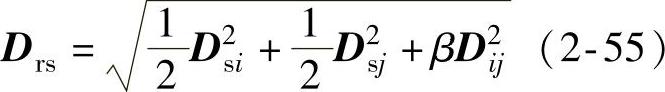
式中，。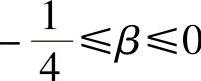

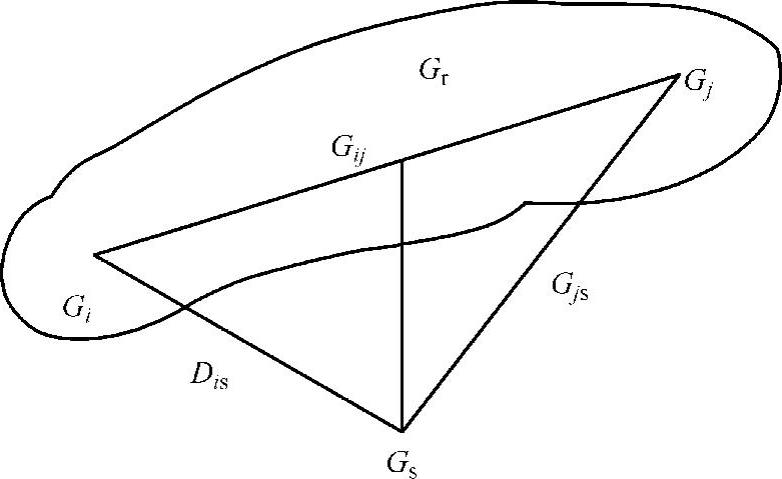
图2-7 中间距离法图示

（4）重心法

重心法在定义两类之间的距离时，考虑了每一类中所包含的样品数，即以两类重心之间的距离作为两类之间的距离，设G_i与G_j类中分别含n_i、n_j个样品，其重心分别为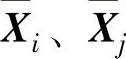，将G_i与G_j合并为G_r类，则G_r中含n_r=n_i+n_j个样品，其重心为

如果类G_s的重心为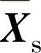，则类G_s与G_r的距离平方为

（5）类平均法

类平均法以两类样品两两之间的距离平方和的平均值确定两类之间的距离平方，即

如果G_i与G_j类合并为G_r，则新类G_r与其他类G_s间的距离平方为

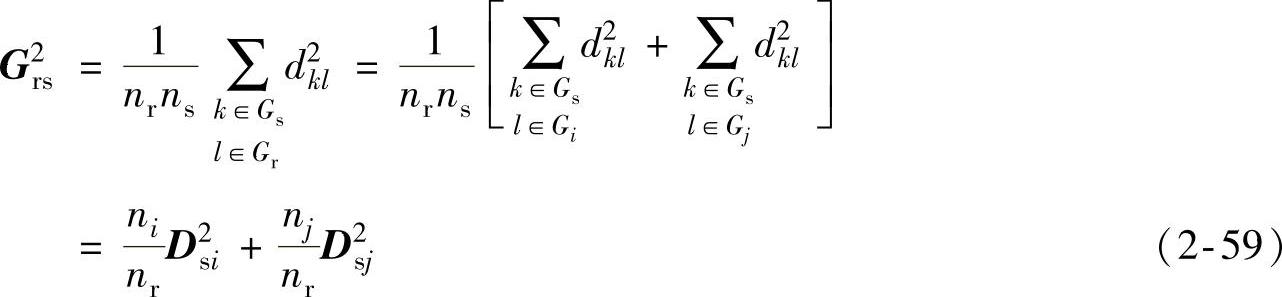
（6）可变类平均法

在类平均法递推公式中，G_i和G_j之间的距离没有反映进去，为修改式（2-59）得到递推公式：

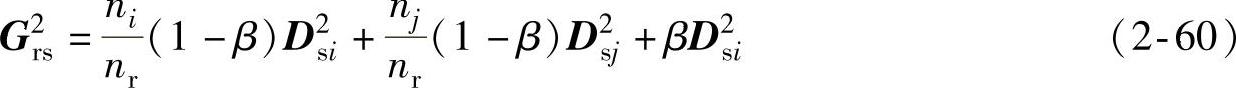
式（2-60）中，β＞0时，有空间压缩作用；当β=0时，聚合空间守恒；当β＜0时，有空间扩张作用。一般情况下，β常取负值，且。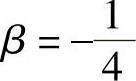

（7）可变法

可变法的递推公式为

式中，β＜1，且常取。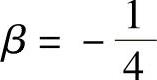

（8）离差平方和法

假定已将n个样品分为k类：G₁，G₂，…，G_k。X_ij表示G_j类中第i个样品，记n_j为G_j中样品数，X_j表示G_j的重心，则G_j中样品的离差平方和为

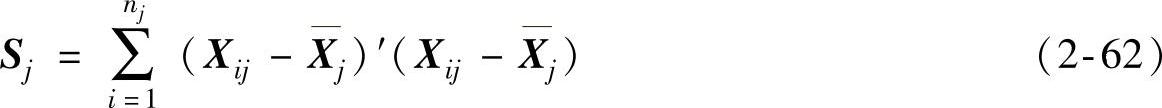
全部k类的平方和为

离差平方和法先将n个样品自成一类，然后每次缩小一类，每缩小一类离差平方和要增大。该方法缩小类的原则是选使S增加最小的两类进行合并，直至所有样品为一类为止。

上述8种聚类方法中，它们并类的原则和步骤是相同的，不同之处在于计算类与类间的距离时选用了不同的定义，从而有不同的递推公式。Wishart1969年提出了统一的递推公式，即

其中，系数α_i、α_j、β、γ对不同的聚类方法取不同的数值，表2-2列出了上述八种聚类方法中α_i、α_j、β、γ在式（2-64）中的取值。

表2-2 系统聚类法统一公式参数表