光程校正的目的是消除光程的变化或样品的稀释所产生的影响。

1.附加散射校正（Multiplicative Scatter Correction，MSC）

在漫反射光谱测量中，由于样品的不均匀性（粒度分布）常导致所测的样品光谱具有很大的差异性，即使相同的样品，多次测量的光谱也会出现差异，此即光散射现象。在许多情况下，散射引起的光谱变化可能要大于样品成分引起的光谱变化。散射的程度与光的波长、颗粒度和样品的折射指数有关，因此在整个光谱范围内，散射的强度是不同的，通常表现为基线的平移、旋转、二次和高次曲线，在长波近红外情况下这种影响表现得尤为明显。

MSC是由Geladi等人提出的，目的是校正每个样品的散射并获得较“理想”的光谱。MSC假定与波长有关的散射对光谱的贡献和对成分的贡献是不同的，理论上说，通过光谱上许多点的数据分析，可以把这两部分分开。MSC方法认为每一条光谱都应该与“理想”光谱成线性关系，而真正的“理想”光谱无法得到，可以用校正集的平均光谱来近似。因此每个样品在任意波长点下反射吸光度值与其平均光谱的相应吸光度呈近似线性关系，直线的截距和斜率可由光谱集线性回归获得，并用以校正每条光谱，截距（即附加效应）大小反映样品反射效果而斜率大小则反映样品的均匀性。具体计算公式如下：

平均光谱：

线性回归：

MSC校正：

上述公式中，A是校正集光谱矩阵，A_i为第i个样品的光谱，m_i和b_i是第i个样品光谱A_i与平均光谱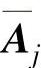的线性回归的斜率与截距，都是列矢量。通过调整m_i和b_i的不同，使得在减少光谱差异的同时尽量保留与化学成分相关的信息。这并不是说经MSC校正的光谱就是样品的真实光谱，只能说通过这样的校正，随机变异得到最大可能的扣除。(www.daowen.com)

2.标准正态变量变换（StandardNormalizedVariate，SNV）

SNV校正也是用来校正样品间因散射引起的光谱差异。但与MSC有所不同，SNV校正认为每一个光谱中，各波长点的吸光度值应满足一定的分布（如正态分布），通过这一假设对每一条光谱进行校正，无需“理想”光谱。SNV是原光谱减去该光谱的平均值μ后，再除以该光谱数据的标准偏差σ（标度化，scaling），实质是使原光谱数据标准正态化，即

消除趋势（Detrending）方法如下：对SNV校正后的光谱矩阵A^SNV_n×p的每一条样品光谱，拟合出一个二次多项式，然后将A^SNV_n×p的每一条样品光谱减去对应的二次多项式，即可去除趋势。消除趋势一般与SNV一起使用，很少单独使用。

3.归一化（normalization）处理

在建立近红外光谱定标分析模型时，需将光谱的特征与待测样品的性质或结构特征相互关联。正是基于如上的特点，在建立NIR定量或定性模型前，往往需要采用一些数据增强算法来降低直至消除一些冗余信息，从而在降低样品间相关性的同时，也能够增大样品之间的差异，进而达到提高模型的重现性和预测能力的效果。主要采取归一化（normalization）算法等。该方法的基本思路是计算每个样品的平均值，将光谱数据减去这些数值，使所有样品的有关数据都分布在零点两侧，充分反映变化信息，这样，温度或人为操作等客观因素所带来的变化对光谱数据造成的影响可以有效的被去除，并且对以后回归运算有一定的简化作用。具体算法是

式中，y_i表示原始光谱；y表示光谱的均值。

这样处理后的光谱数据充分反映了信息变化，所有数据都分布在零点两侧，简化并稳定了以后的回归运算。