马氏距离法可以用来剔除异常样品，计算原理如下所示。当C_x满秩时，样品与光谱X_c重心之间的马氏距离定义为

其中，x表示平均光谱；C_x是X的方差-协方差矩阵。

马氏距离法是度量样品与中心之间距离的一种有效途径，已被应用到光谱的聚类分析中。计算马氏距离不仅照顾了相同波长点光谱信号的变化（方差），还考虑了不同波长点光谱间的变化（协方差）。

设光谱数据为A（n×k）矩阵，n为样品数，k为选出的主成分数。马氏距离算法分为以下步骤：

1）计算n个样品的平均光谱：

式中，A为光谱矩阵；j为波长序号；n为样品数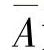；为平均光谱。

2）把近红外光谱矩阵进行中心化处理：(www.daowen.com)

3）计算得到马氏矩阵：

此时的波长数为k，所以M是k×k维矩阵。

4）计算校正集各个样品到平均光谱的马氏距离：

5）根据计算出的n个马氏距离设置一个阈值来检验异常样品的存在，计算方法为

式中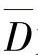，为马氏距离平均值；e为调整闭值范围参数，σ_D为马氏距离标准差。

如果D_i≤D_t，则样品i与样品的平均光谱很接近，则称i为平均样品的邻近样品。令N_i为i的邻近的样品个数，N_i值越大，样品i的邻近的样品数越多，在空间上越密集。可以设置不同的阈值范围参数e，来调节N_i值的大小，e值越大，N_i值越大，阈值的范围越宽，邻近样品空间上的密集度就会越高；反之亦然。