主成分分析（Principle Component Analysis，PCA）法可以把多个指标化为几个综合性指标，被广泛应用到各领域。在实际问题中，研究多指标（变量）问题时，不同指标之间具有一定相关性，由于多指标及指标之间有相关性，从而增加了分析问题的复杂性。PCA就是将原来具有一定相关性的指标，组合成的一组新的相互无关的综合指标来代替原来的指标。对近红外光谱进行主成分分析，能够达到对光谱矩阵进行降维的目的，不会过多地丢失光谱所含有的信息，同时还能够减少原始近红外光谱的冗余信息。

设样品观测数据矩阵为X，则PCA具体计算步骤如下：

其中，

该矩阵为n个样品p个波长上的光谱信息阵，记X的样品均值、样品协差矩阵以及相关阵分别为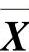、S和R，通过由样品信息阵X出发，构造原各波长点光谱信息变量的线性组合但不相关，且具有最大的样品方差，就是构造样品主成分。

第一样品主成分=线性组合l′₁X_j，满足‖l₁‖=1，且l′₁X_j的样品方差最大（其中，X_j为在新坐标系下的第j个观测值，l为其系数）；

第二样品主成分=线性组合l′₂X_j，满足‖l₂‖=1及l′₂X_j与l′₁X_j样品协方差为0，且使l′₂X_j的样品方差最大。

一般地，第i个样品主成分=线性组合l′_iX_j，满足‖l_i‖=1得l′_iX_j与l′_kX_j（k＜i）的样品协方差为0，且使l′_iX_j的样品方差最大。

1）对原始数据进行标准化处理：

式中，；。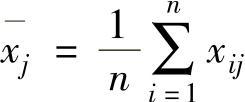

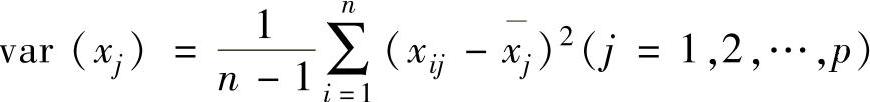2）计算样品相关系数矩阵：(www.daowen.com)

为了方便，假定原始光谱数据标准化后仍用X表示，则经过标准化处理的数据的相关系数为

3）求R的特征值（λ₁，λ₂，…，λ_p）及其相应的特征矢量a_i=（a_i1，a_i2，…，a_ip），i=1，2，…，p。

4）选择重要主成分，并列出其主成分表达式。

通过主成分分析能够得到p个主成分，但是，由于各个主成分包含的信息量随着方差的递减而递减，所以在实际分析过程中，一般不选取p个主成分，而是通过分析各个主成分的累计贡献率大小来选取前m个主成分，贡献率是指某个特征值占全部特征值的比重，如下：

5）取前m个较大的特征值对应特征矢量来构成变换矩阵T^T：

T^T=（a₁，a₂，…，a_m）m＜n （2-10）

6）通过

Y=TX （2-11）

计算前m个主成分，从而达到降低维数的目的，依据成分得分的数据，则可以进行进一步的统计分析。