下面介绍一种分析方法^[31]，假设心轴（或定位销）没有形状误差，工件和心轴为绝对刚体。

1）工件定位孔表面的形状为抛物线波纹状，工件在间隙圆柱心轴上的接触情况如图2-42a所示。

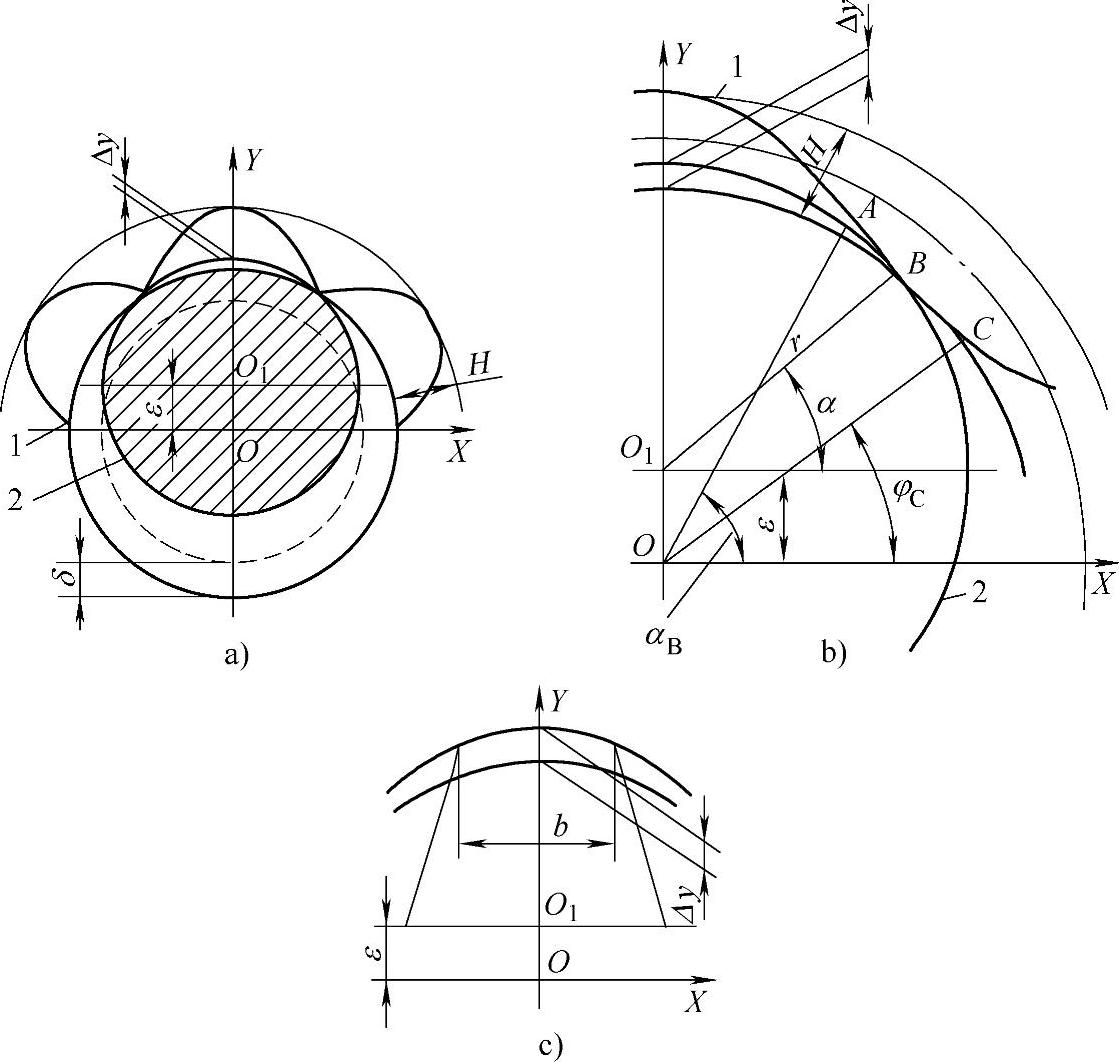
图2-42 有表面形状误差的孔在心轴上的定位

1—工件孔表面 2—心轴

按下式计算抛物线波谷曲率半径：

R=（R_B+H）²/（R_B+H+Hn²/16200）

当定位心轴半径r＜R时，说明心轴2与工件孔表面1沿波谷接触；当r＞R时，说明二者沿波峰接触，如图2-42a所示。

由图2-42a可知，当心轴与孔沿波谷接触时（r＜R），最大定位误差为

ε_max=δ+H（δ为定位时在半径上工件孔与心轴的间隙）

当r＞R时，由于孔表面波纹度使心轴母线产生偏移Δ_y，这时定位误差为

ε=Δ_y+δ

Δ_y=R_Bcos（180°/n）-rcos{arcsin[（R_B/r）sin（180°/n）]}

式中 R_B——波纹形成的孔半径；

r——心轴的半径；

n——波纹数。(www.daowen.com)

由分析可知，在不同的r、R_B、δ值和n值一定的情况下，相对偏移Δ_y/δ保持一定，不同n值时的Δ_y/δ值如下：

所以当孔表面形状为抛物线波纹形时，如已知孔的波纹数n，即可确定Δ_y值。

2）工件定位孔表面的形状为正弦波纹状（图2-42b）。这时工件定位孔与圆柱间隙心轴可能在波谷、波峰或波纹侧面接触，图中表示在B点接触。这时定位误差的计算与上述相同，即ε=Δ_y+δ，而Δ_y值按下述类比方法求出。

图2-43所示为当工件定位孔（直径为40mm）表面为正弦波纹状时，在不同波纹度高度H和波纹数n的条件下相对偏移Δ_y/H值；并且由图2-44可知，孔直径大小对Δ_y/H的影响很小，所以图2-43也适合于各种直径。

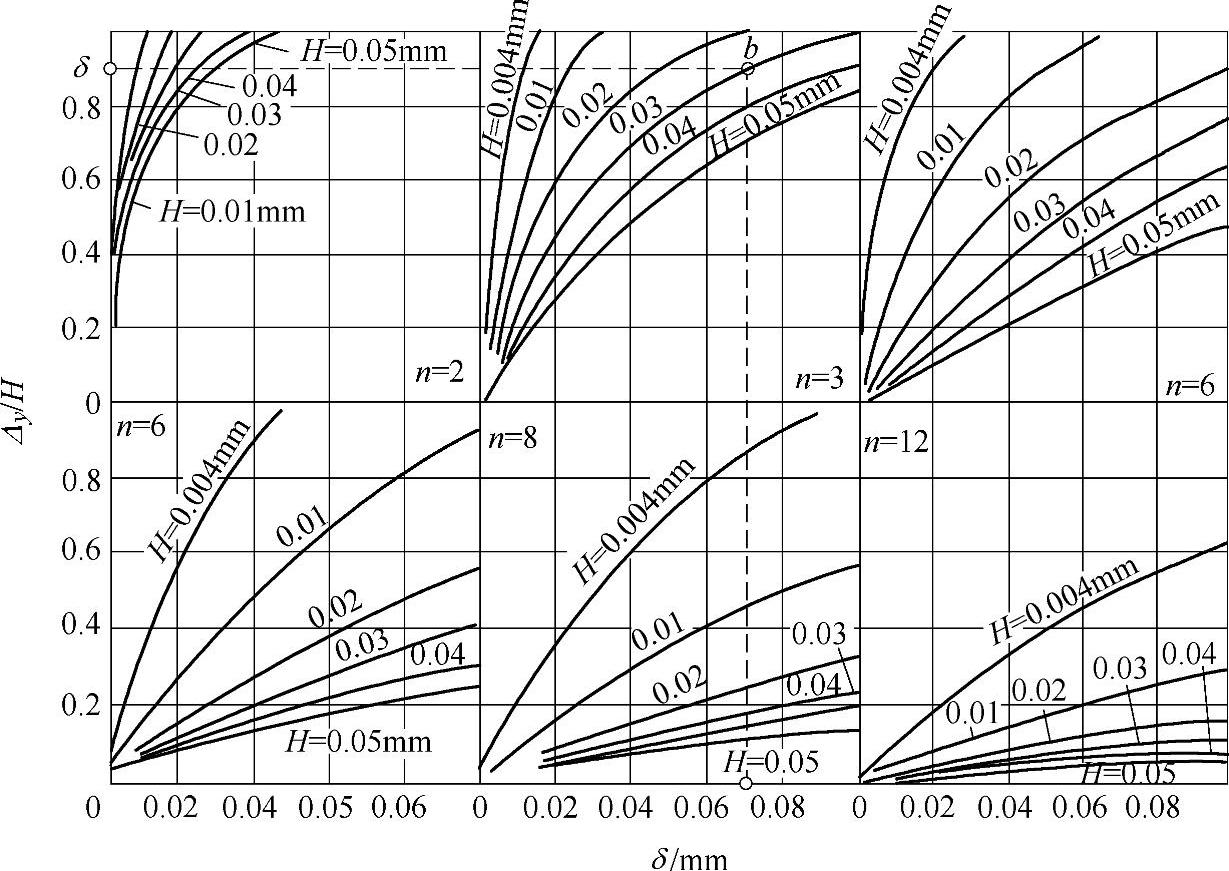
图2-43 波纹高度H和波纹数n与相对偏移Δ_y/H的关系

现举例说明图2-43的应用。工件定位孔直径D=75^+0.12₀mm，孔表面有正弦形波纹：H=0.03mm、n=3；定位销直径的下极限偏差为0.013mm。这时单边径向间隙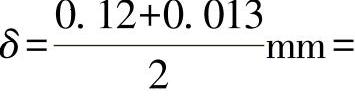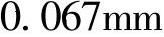，由图2-43按δ=0.067mm、n=3和H=0.03mm查得对应的（Δ_y/H）=0.85，即Δ_y=0.85H=0.025mm，则定位误差ε=Δ_y+δ=0.025mm+0.067mm=0.092mm。

工件定位孔在菱形销上定位（图2-42c）时，由于定位孔表面有正弦形波纹而产生定位误差Δ_y，Δ_y/H值如图2-45所示，图中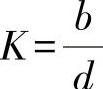：（b为菱形销圆柱部分的宽度；d为菱形销圆柱部分的直径）。

现举例说明图2-45的应用：工件定位孔直径D=8^+0.10₀mm，菱形销圆柱部分直径d=8^-0.020_-0.055mm，定位孔表面正弦波纹数n=2，波纹高度H=0.03mm。由图2-45按n=2和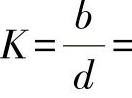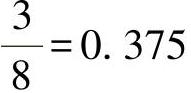查得（Δ_y/H）=0.88，所以Δ_y=0.03mm×0.88=0.026mm，则定位误差。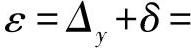

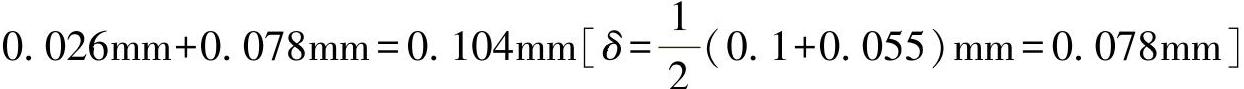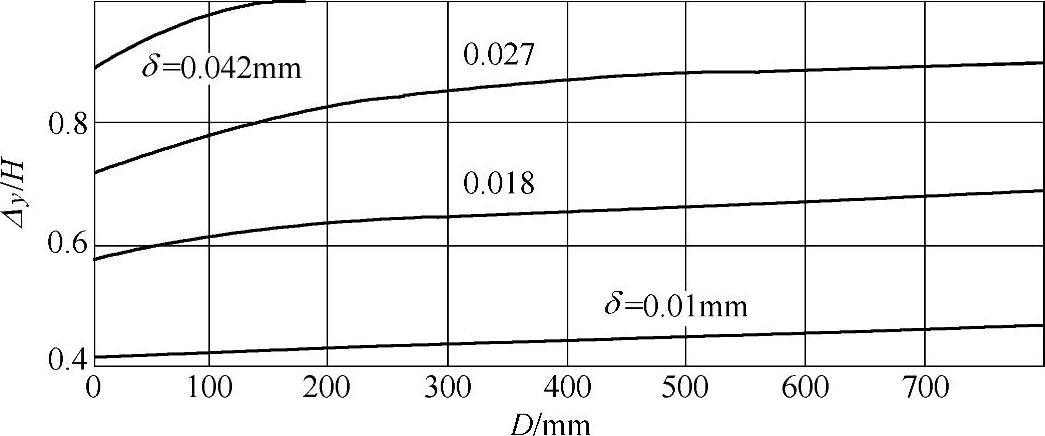
图2-44 在波纹高度H=0.02mm和不同径向间隙δ条件下，

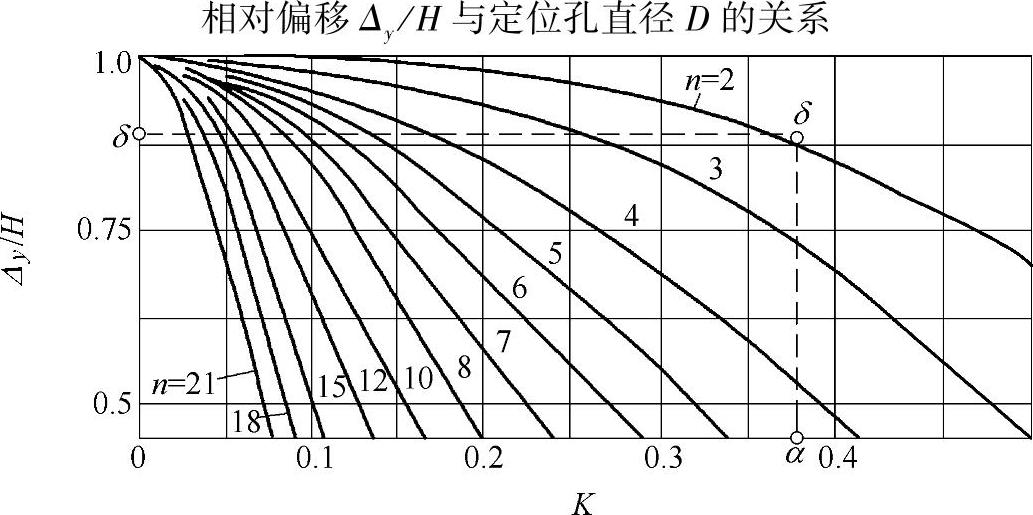
图2-45 定位孔波纹数n和K=b/d值与工件在菱形销上相对偏移Δ_y/H的关系