夹具装夹误差在很多情况下是加工误差中的主要部分。夹具设计的主要任务之一是确定夹具定位误差和夹紧误差，即确定夹具的装夹误差。

1.工件的定位误差和计算

工件的定位误差是指工件的定位基准在夹具上的实际位置与要求理想定位基准位置的差异，该差异使工件对理想位置产生加工误差，而各个工件的差异不同，从而使一批工件产生分散性。

产生定位误差的因素有：由于工件基准面本身尺寸和形状有误差，使工件定位基准产生偏移；有时由于工件在夹具上实际所用的定位基准与产品图样或工艺要求的基准不同而产生的定位基准不重合；以及由于夹具定位元件尺寸和形状有误差等。

在实际工作中，对具体加工情况的定位误差应作具体分析。本章主要介绍各种定位方法的定位误差。下面先举例说明定位误差分析和计算的基本方法和概念。

（1）单坐标方向基准偏移或不重合产生的定位误差 当加工尺寸只与一个定位元件有关（例如铣平面时以底面定位，只要求尺寸高度合格），或其他定位方向误差很小，可以忽略时，这时可只分析单坐标方向（即加工方向）的定位误差。

例如对图2-5a，加工尺寸H，以平面A定位，定位基准与设计基准重合，则定位误差ε_h=0（这时考虑定位面的形状误差相对于尺寸误差很小，可忽略）。

加工尺寸t，由于工件在夹具上的定位面A与尺寸t的设计基准面不重合，尺寸t的定位误差ε_t=±δ（±δ为尺寸H的公差）。在加工尺寸链中，t是封闭环，H和（H-t）是组成环，可得各环的公差关系δ+δ_H-t=δ₁，即δ+δ_h1=δ₁，δ_h1=δ₁-δ。

所以为保证尺寸t在公差±δ₁内，必须控制尺寸（H-t）=h₁的公差在±（δ₁-δ）内。如尺寸H=50±0.06mm，t=20±0.10mm，则尺寸h₁=（H-t）=30mm的制造公差应在±（δ₁-δ）=±（0.10-0.06）mm=±0.04mm内。

上面是按极限法计算定位误差的，具有较大的保险性和有一定的精度储备，但有时会对加工提出较高的要求，甚至难以达到，所以根据具体情况可用均方根法计算。

图2-5b所示为工件，以外圆在V形块上定位，当采用长V形块时，限制了工件七个自由度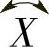、、、Z↓；采用窄V形块时，限制了工件三个自由度、Z↓。工件的外圆直径为D⁰_-δ，若工件的圆度误差很小，可不考虑，也可不考虑V形角的误差，一批工件中心在垂直方向的偏移为ε₀，外圆上母线点的偏移为ε₁，下母线点的偏移为ε₂，由图2-5b可得

同样可得

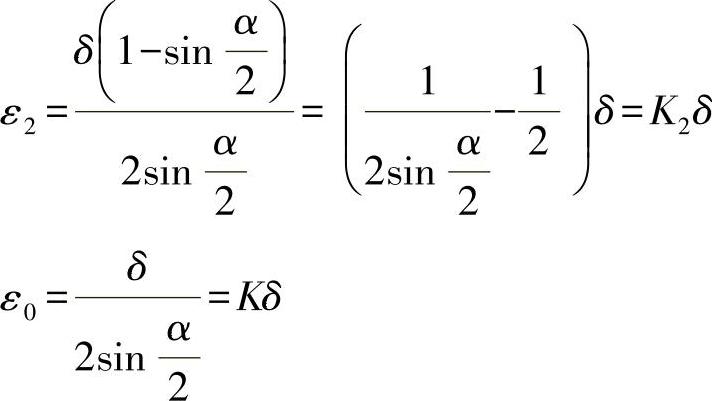
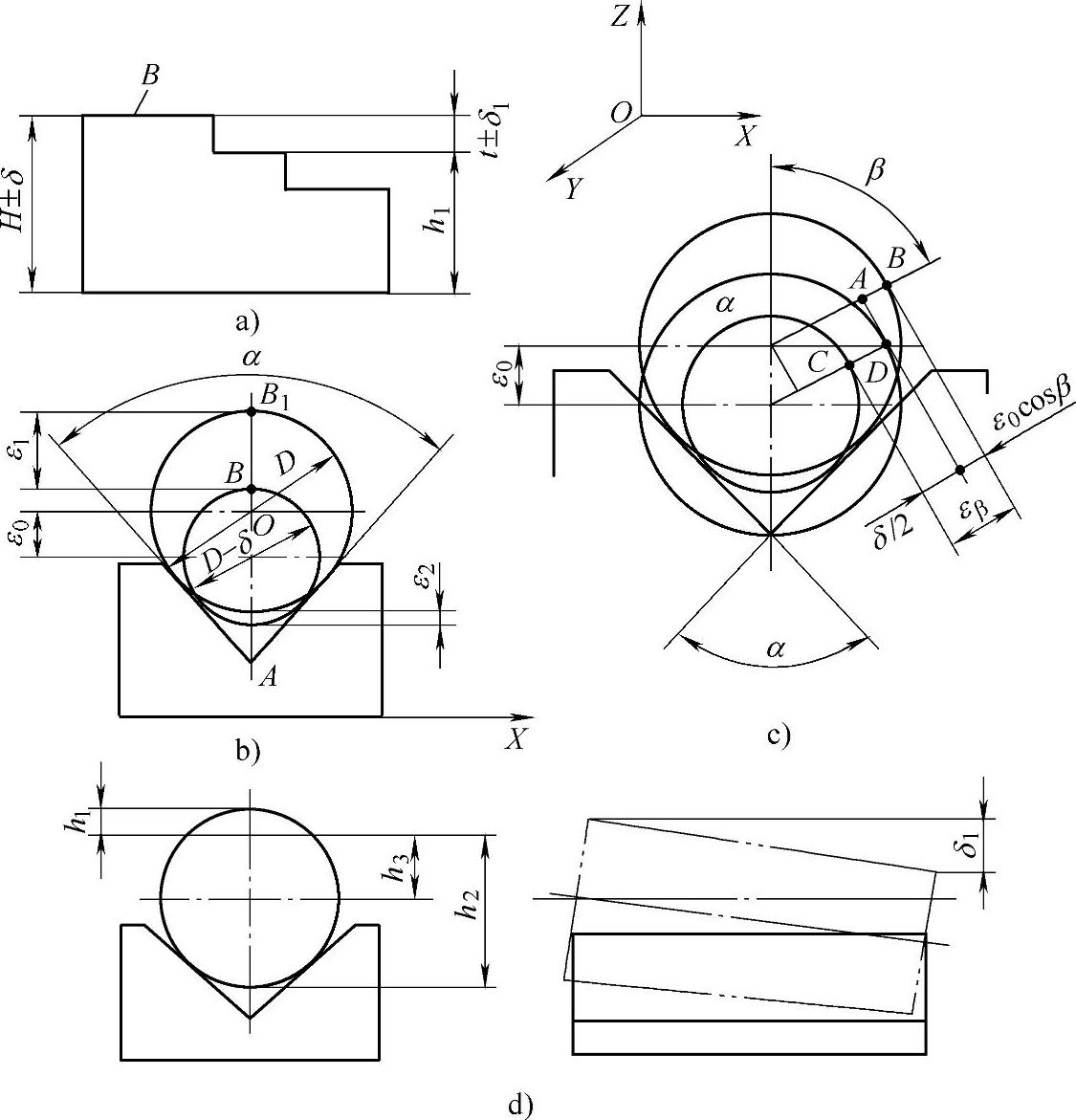
图2-5 工件的定位误差分析图

外圆以不同V形角和以平面定位时（α=180°）的K、K₁、K₂值见表2-1。

表2-1 计算ε₀、ε₁、ε₂时的系数K、K₁、K₂的值

工件在V形块上定位，中心O在垂直方向有定位误差（由于直径变化），但在水平方向工件中心没有定位误差，这是用V形块定位的特点。

下面介绍工件外圆上与垂直方向呈β角的任一点由于工件直径公差δ产生的定位误差ε_β的计算，由图2-5c可得

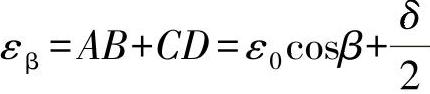
由前述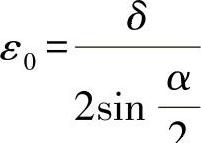

所以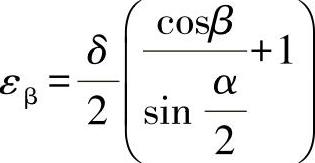

（2）多坐标方向的定位误差 当以多个元件在夹具不同方向同时以工件多个表面定位（可称为组合定位，实际上工件的定位大多是组合定位）时，除分析加工尺寸方向的定位误差外，还要考虑定位面其他方向的误差对加工尺寸定位误差的影响。

图2-5d所示的工件加工尺寸为h₁、h₂和h₃，若不考虑工件长度方向的定位误差，则其定位误差（Kδ）分别为1.21δ、0.21δ、0.7δ。若考虑工件在长度方向有圆柱度误差，例如有锥度，这将导致工件在V形定位块上产生倾斜，产生定位误差δ₁。本例δ₁与δ在同一方向，所以总的定位误差为δ′=Kδ+δ₁。

在夹具中，工件在三个坐标方向定位，由于工件的各定位基准面有尺寸和形状误差，以及夹具定位元件的制造误差，所以工件的定位误差具有立体空间性。

图2-6表示工件定位面上的点A（坐标为x，y，z）对坐标X、Y、Z有微小转角（偏斜）误差θ_X、θ_Y、θ_Z和微小平移Δ_X、Δ_Y、Δ_Z。图示转角和平移朝坐标正方向，实际也可能朝另一方向。

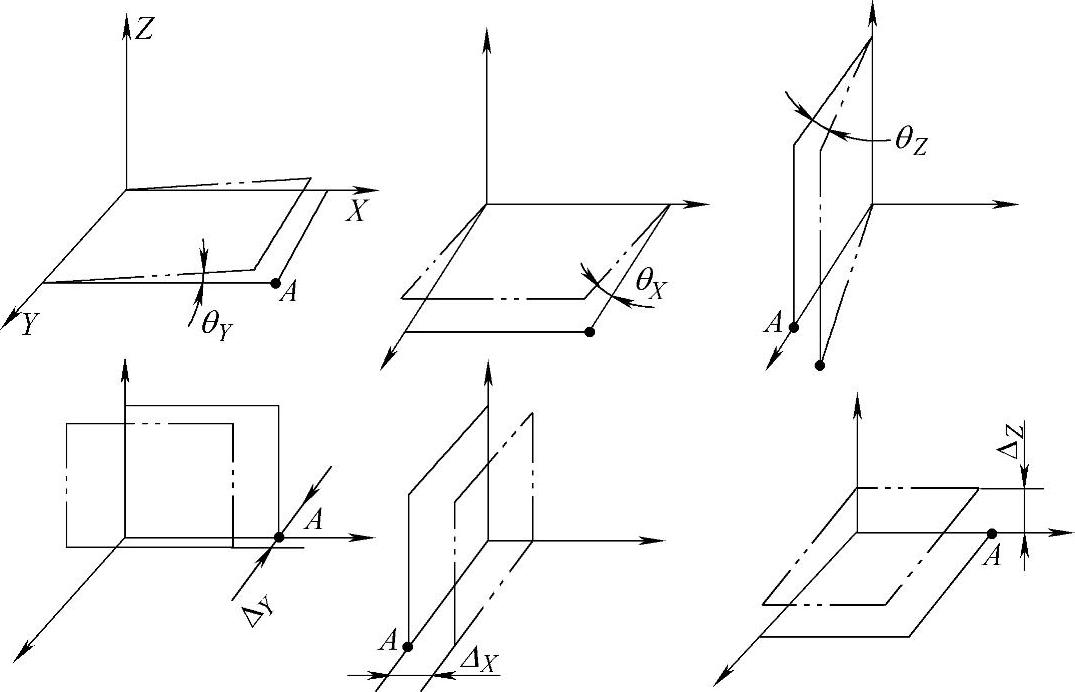
图2-6 夹具转角和平移定位误差

按下列各式计算工件上任意一点在各坐标方向上的定位误差分量

δ_X=yθ_Z+zθ_Y+Δ_X （2-1）

δ_Y=xθ_Z+zθ_X+Δ_Y （2-2）

δ_Z=xθ_Y+yθ_X+Δ_Z （2-3）

式中 x、y、z——加工表面上任一点坐标；

θ_X、θ_Y、θ_Z——工件定位点所在平面对各坐标的微小转角，θ_X≈sinθ_X，θ_Y≈sinθ_Y，θ_Z≈sinθ_Z；

Δ_X、Δ_Y、Δ_Z——工件定位面对各坐标的平移定位误差。

工件上所求点对坐标原点距离的总误差为

以图2-7a为例，加工工件尺寸40±0.3mm，定位基准面A与设计基准面不重合，产生的定位误差为0.2mm（±0.1mm）。若工件A面只对Y轴有正弦为0.03/100的转角，即sinθ_Y=0.0003，则由式（2-1）计算加工尺寸40±0.3mm的定位误差为（计算时考虑工件侧面定位点到工件底面的距离为50mm，并考虑两个方向转角）

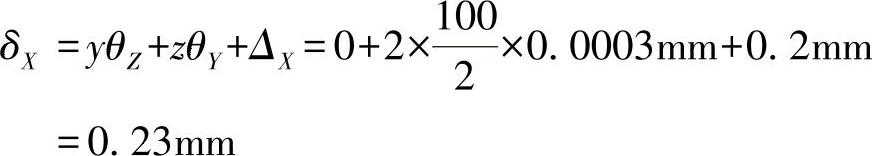(www.daowen.com)

加工尺寸公差为0.6mm（±0.3mm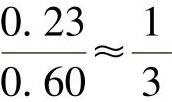），，所以该误差可以接受。

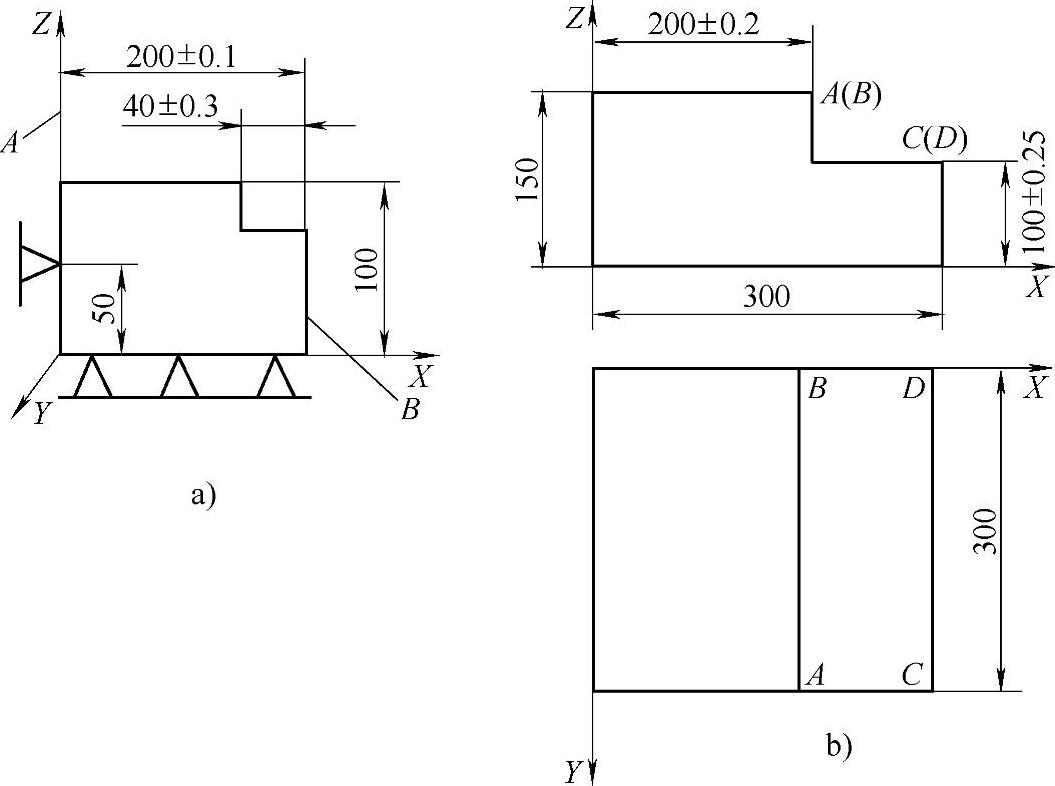
图2-7 加工点定位误差的计算

又如图2-7b所示，用圆铣刀半精铣尺寸200±0.2mm和尺寸100±0.25mm，加工精度等级为IT10。若工件各定位面分别绕X、Y、Z轴的转角正弦值均为0.0002，计算尺寸200mm和尺寸100mm的定位误差δ_XA、δ_XB、δ_ZC和δ_ZD。各点坐标分别为：A（200，300，150），B（200，0，150），C（300，300，100），D（300，0，100）。这时Δ_X、Δ_Y、Δ_Z=0。

计算时考虑两个方向的转角误差。

按式（2-1） δ_XA=yθ_Z+zθ_Y+Δ_X

=±（300×0.0002+150×0.0002+0）mm=±0.09mm

δ_XB=±（0+150×0.0002+0）mm=±0.03mm

按式（2-3） δ_ZC=xθ_Y+yθ_X+Δ_Z

=±（300×0.0002+300×0.0002+0）mm=±0.12mm

δ_ZD=±（300×0.0002+0+0）mm=±0.06mm

δ_XA与尺寸200±0.2mm公差的比值为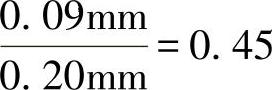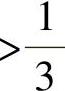，。这时再按第一章的式（1-2）验算定位误差是否小于允许的定位误差ε_L=T-ω（T为工件尺寸公差，ω为加工该尺寸的加工精度）。

尺寸200mm的公差为0.4（±0.2）mm，加工公差等级为IT10，ω=0.185mm，ε_L=0.40mm-0.185mm=0.215mm≈±0.11mm＞δ_XA=±0.09mm。可知按极限法计算的δ_XA可以接受。

δ_ZC与尺寸100±0.25mm公差的比值为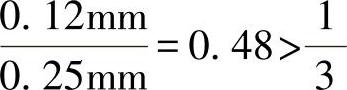，这时ε_L=0.50mm-0.16mm=0.34mm=±0.17mm＞δ_ZC=±0.12mm，所以也是可以接受的（对尺寸100mm和IT10，ω=0.160mm）。

2.工件的夹紧误差

工件的夹紧误差是指工件夹紧后定位基准有变形和夹紧力不稳定，使工件产生的定位误差。如果夹紧力稳定，夹紧力主要影响加工尺寸分散中心的坐标，不会产生明显的尺寸分散性；如果夹紧力不稳定，则一批工件会产生较大的尺寸分散性。

图2-8所示为工件的夹紧误差。当工件与夹具定位支承面的接触变形为最小时（即定位支承面的压缩量最小，处于m′n′位置），加工出的尺寸为H′；当夹紧力增大后，工件定位支承面处于m″n″位置，加工出的尺寸为H″。这时产生尺寸分散性（H″-H′），工件的公称尺寸H在H″～H′内变化，产生的夹紧误差为ε_c=H″-H′。

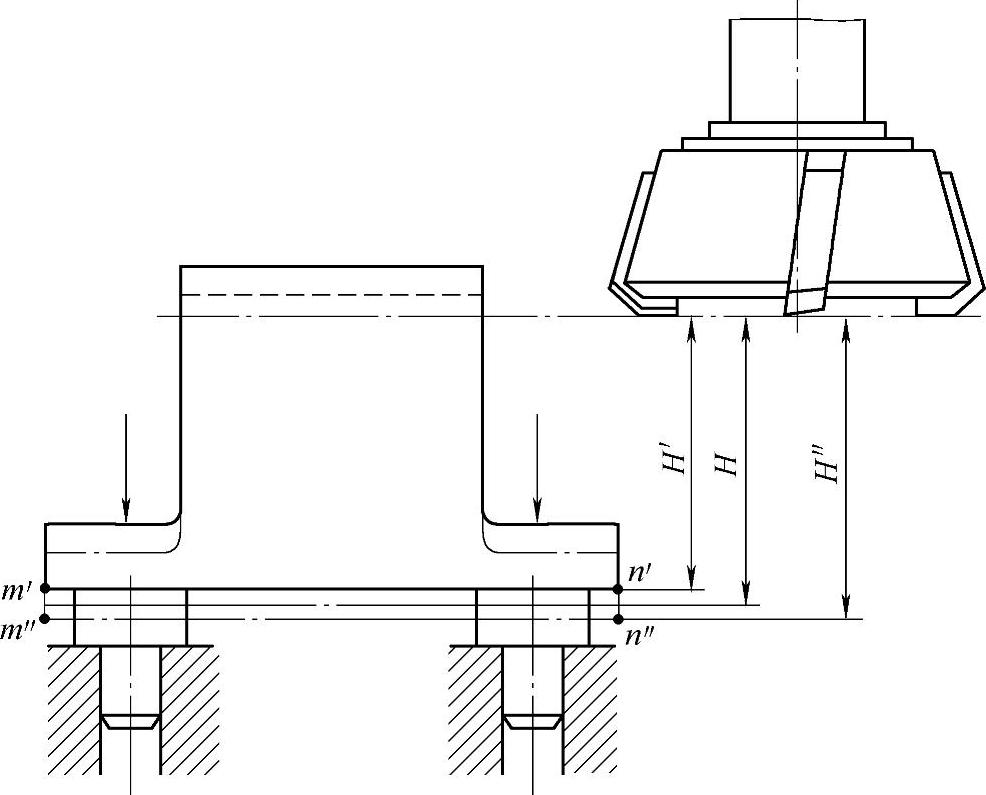
图2-8 工件的夹紧误差

3.工件的装夹误差

工件先定位后夹紧，夹紧后的工件定位基准对理想位置的偏移就是工件的装夹误差ε_Lc。如果夹紧误差与定位误差方向一致，则ε_Lc=ε_L+ε_c。

若夹紧误差与定位误差的方向是随机的，则

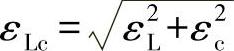
若一个工件在几个夹具上加工相同的部位，则装夹误差还应考虑各夹具之间的定位差异ε_L′，这时装夹误差为

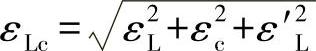
对同时夹紧和定位的夹具，例如自定心卡盘、弹性夹头等，直接以装夹误差表示其定位和夹紧的精度，工件的装夹误差数据主要由试验确定。在本章中在介绍各种定位方式时，将介绍夹紧误差对定位误差的影响和装夹误差的数据。

夹紧误差（单位为μm）的一般计算式为^[19]

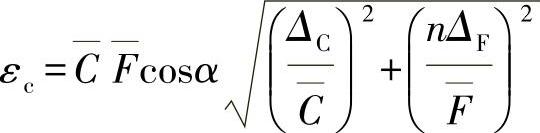
式中 ——与材料和接触形状有关的系数C的平均值（见表3-119）；

F——作用在支承上的平均力，单位为N；

Δ_C和Δ_F——系数C和力F的极限分散值；

n——系数（见表3-119）；

α——最大接触变形方向与定位尺寸方向之间的夹角。

考虑工件基面硬度和表面粗糙度的变化Δ_HB和Δ_Rz

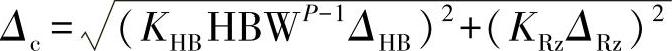
式中 K_HB和K_Rz——各种支承的值，见表3-119；

P——支钉、平板支承P=1，V形支承P=-1；

HBW——硬度值。

平面定位支承、V形块、中心孔等夹紧时的接触变形的计算见第3章表3-117～表3-119。