（一）口诀

复杂电路变简单，可将星角来变换。

变时一点要牢记，外接三点不能变。

星变角时求某边，两两积和除对面。

角变星时求某枝，两臂之积除和三。

（二）说明

1.概述

不能使用串联或并联的关系进行电阻计算的电路被称为复杂电路，最简单的复杂电路是图1-8所示的桥式电路。

对于复杂电路，可先将其中连成星形（三个电阻有一个公共的连接点时，称为星形联结，可用符号“”表示）的三个电阻（如图1-8中的R₁、R₂和R₃）转化成三角形电路（三个电阻依次连接成为一个闭合回路时，称为三角形联结，可用符号“△”表示），或将其中连成三角形的三个电阻（如图1-8中的R₁、R₃和R₄）转化成星形电路，这就是所谓的电阻星-三角变换问题。进行上述变换后，原有的复杂电路就会转变为简单电路，再用串、并联的计算方法求出总电阻值。电阻星-三角变换的理论推导相对较复杂，在此不准备给出。本题只给出转换方法口诀和使用方法举例。

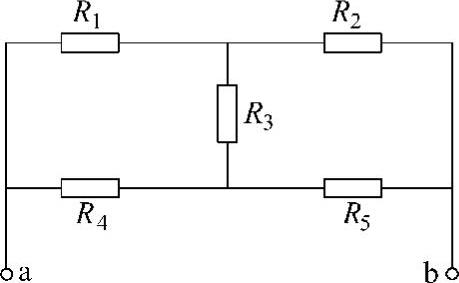
图1-8 最简单的复杂电路——桥式电路

2.口诀说明

设星形联结的三个电阻分别是R₁、R₂和R₃，等效转换三角形联结的三个电阻分别是R₁₂（对应星形联结的R₁和R₂）、R₂₃（对应星形联结的R₂和R₃）和R₃₁（对应星形联结的R₃和R₁），参照图1-9说明转换口诀的使用方法。

（1）当由星形联结转换成三角形联结时，口诀为“星变角时求某边，两两积和除对面”。这里的“两两”是指星形联结时的每两个电阻，“两两积和”即为（R₁R₂+R₂R₃+R₃R₁）；“对面”是指与转换成三角形联结以后的一个电阻相对的原星形联结的那个电阻，如图1-9中R₁₂的“对面”应是R₃。设R_LJH=（R₁R₂+R₂R₃+R₃R₁），由此可得到由星形联结转换成三角形联结时的三个电阻计算公式为

R₁₂=（R₁R₂+R₂R₃+R₃R₁）/R₃

=R_LJH/R₃（1-12）

R₂₃=（R₁R₂+R₂R₃+R₃R₁）/R₁

=R_LJH/R₁（1-13）

R₃₁=（R₁R₂+R₂R₃+R₃R₁）/R₂

=R_LJH/R₂（1-14）

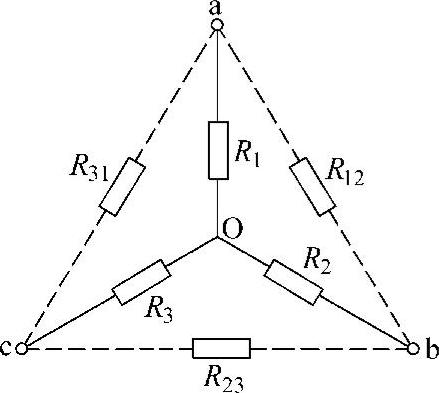
图1-9 电阻的星-三角变换电路

（2）当由三角形联结转换成星形联结时，口诀为“角变星时求某枝，两臂之积除和三”。这里的“两臂”是指与转换成星形联结的一个电阻（后面称为“一枝”，如R₁）同一个顶点的三角形联结时的两个电阻（如对应R₁的两臂是R₁₂和R₃₁），“和三”即为三角形联结时三个电阻之和，即（R₁₂+R₂₃+R₃₁）。设R_HS=（R₁₂+R₂₃+R₃₁），由此可得到由三角形联结转换成星形联结时的三个电阻计算公式为

R₁=R₁₂R₃₁/（R₁₂+R₂₃+R₃₁）

=R₁₂R₃₁/R_HS（1-15）

R₂=R₁₂R₂₃/（R₁₂+R₂₃+R₃₁）

=R₁₂R₂₃/R_HS（1-16）

R₃=R₂₃R₃₁/（R₁₂+R₂₃+R₃₁）(www.daowen.com)

=R₂₃R₃₁/R_HS（1-17）

（三）计算举例

以图1-10a所示的电路图为例，用两种转换方法求取a、b两点之间的电阻R_ab的阻值。

解：（1）用由星形联结转换成三角形联结的方法

第一步：找出R₁、R₂和R₃组成的星形联结与其他电路连接的三个点e、f、d。以这三个点为三角形的三个顶点，画出三个电阻R₁₂、R₂₃和R₃₁（最好用与原图颜色不同的笔）。如图1-10a所示。这一步是口诀中“变时一定要牢记，外接三点不能变”的含义。

第二步：按口诀“星变角时求某边，两两积和除对面”一一求出R₁₂、R₂₃和R₃₁。

为了计算方便，先求出口诀中所提到的“两两积和”，即R_LJH=（R₁R₂+R₂R₃+R₃R₁），再求R₁₂、R₂₃和R₃₁，单位均为Ω。

R_LJH=R1R2+R₂R₃+R₃R₁

=（1×2+2×3+3×1）Ω=11Ω

R₁₂=R_LJH/R3=（11/3）Ω=3.67Ω

R₂₃=R_LJH/R1=（11/1）Ω=11Ω

R₃₁=R_LJH/R2=（11/2）Ω=5.5Ω

第三步：将原有的R₁、R₂和R₃去掉，即成了图1-10b所示的只有串联和并联的简单电路，R₃₁和R₄并联后的电阻与R₂₃和R₅并联后的电阻串联，得到一个电阻值后，再和R₁₂并联，得出最终结果。由此可以求得（计算过程从略）：

R_ab≈2.24Ω

（2）用由三角形联结转换成星形联结的方法

第一步：找出R₁、R₃和R₄组成三角形的与其他电路连接的三个点e、c、d。以这三个点为星形联结的三个顶点，画出三个电阻R₆、R₇和R₈（最好用与原图颜色不同的笔），如图1-10c所示。这一步是口诀中“变时一定要牢记，外接三点不能变”的含义。

第二步：按口诀“角变星时求某枝，两臂之积除和三”一一求出R₆、R₇和R₈。

为了计算方便，先求出口诀中所提到的“和三”，即本例为R_HS=（R₁+R₃+R₄），再求R₆、R₇和R₈，单位均为Ω。

R_HS=R₁+R₃+R₄=（1+3+4）Ω=8Ω

R₆=R₁R₄/R_HS=（1×4/8）Ω=0.5Ω

R₇=R₁R₃/R_HS=（1×3/8）Ω=0.375Ω

R₈=R₃R₄/R_HS=（3×4/8）Ω=1.5Ω

第三步：将原有的R₁、R₃和R₄去掉，即成为了图1-10d所示的只有串联和并联的简单电路，R₇和R₂串联后的电阻与R₈和R₅串联后的电阻并联，得到一个电阻值后，再和R₆串联，得出最终结果。由此可以求得R_ab≈2.24Ω（计算过程从略）。

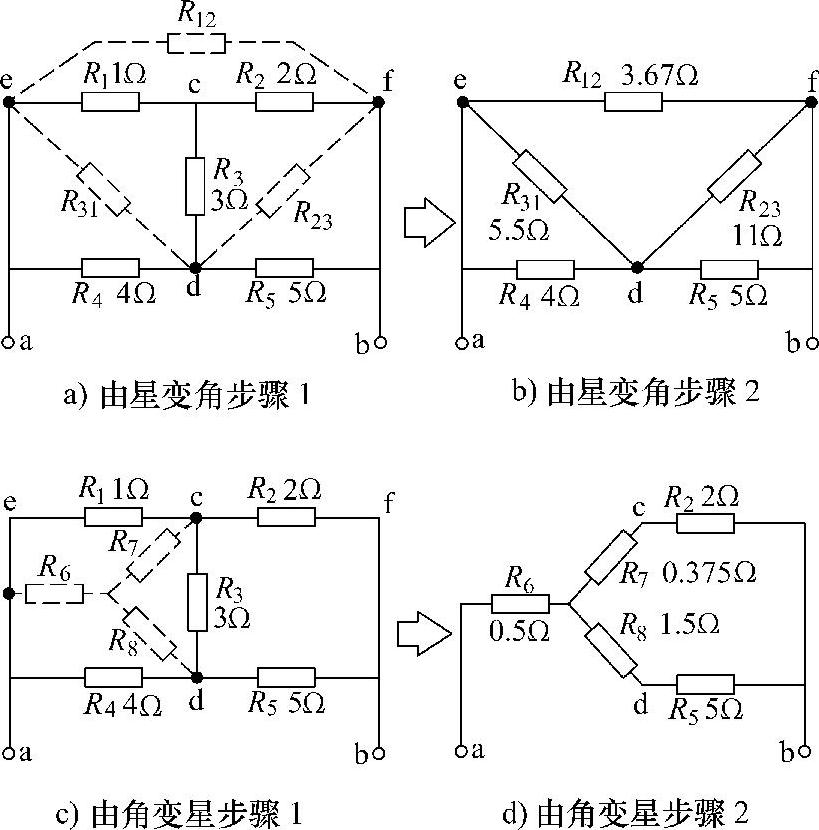
图1-10 用星-三角变换的方法求桥式电路的电阻

从上述计算可知，两种方法所求得的结果相等，也就是说是等效的。在具体使用中，可根据情况选择其中的一种。