（一）口诀

电阻串联值相加，越串越长阻越大。

电阻并联值减小，相当截面在增大。

并联总阻较难求，各值先要求倒数，

倒数之和的倒数，就是并联后电阻。

并联只有俩电阻，总阻可用简式求，

两阻之积作分子，两阻之和作分母。

（二）说明

在电工实际作业中，特别是在处理家用电器和电路控制设备的故障时，经常要遇到电阻的串并联问题。所以必须熟练地掌握相关计算方法，本部分口诀只讲到了总电阻的求取方法，以后还要介绍电压、电流以及功率的计算和相互之间的关系。

用R₁、R₂、R3、…、R_n分别代表将要连接在一起的各个电阻，用R_串代表串联后的总电阻，R_并代表并联后的总电阻，则有如下的计算关系式：

R_串=R₁+R₂+R₃+…+R_n （1-8）

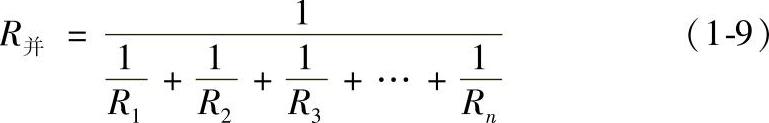
或

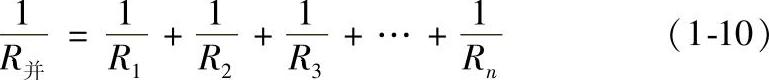
当只有R₁和R₂两个电阻并联时，

（三）计算实例

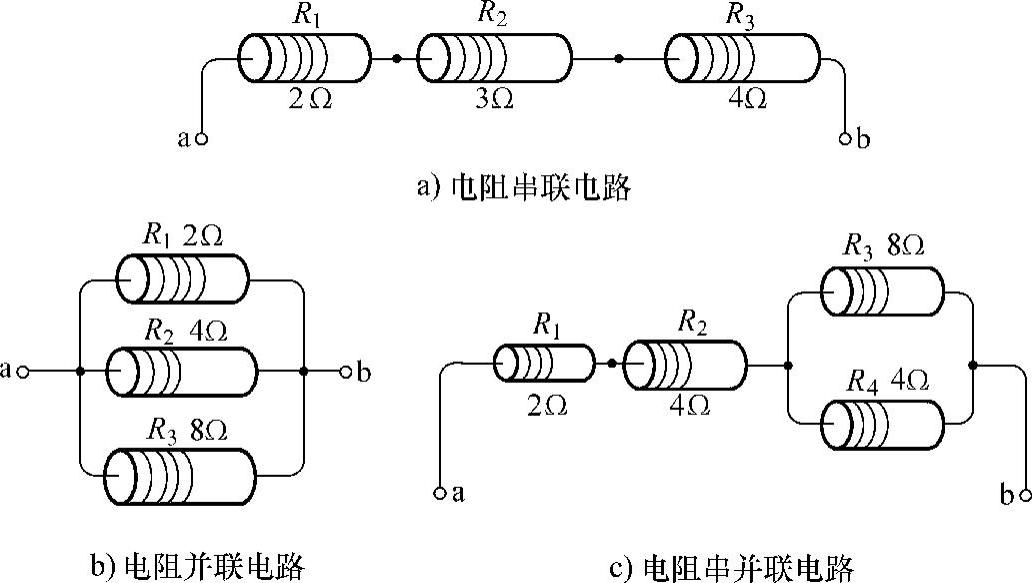
图1-7给出了三个电路图，请计算每个电路中a、b两端点之间的电阻R_ab的数值。

(www.daowen.com)

图1-7 电阻串并联计算实例

解：a）本题图为三个电阻串联，三个电阻分别为R₁=2Ω；R₂=3Ω；R₃=4Ω。根据口诀“电阻串联值相加，越串越长阻越大”和式（1-8）可得：

R_ab=R₁+R₂+R₃=2Ω+3Ω+4Ω=9Ω

b）本题图为三个电阻并联，三个电阻分别为R₁=2Ω；R₂=4Ω；R₃=8Ω。根据口诀“各值先要求倒数，倒数之和的倒数，就是并联后电阻”和式（1-10）可得：

先求出三个电阻的倒数和，即

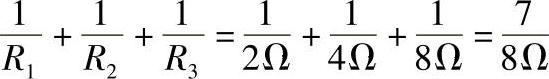
再求出上述结果的倒数，即用1除以上述结果，若上述结果是分数，则将其分子分母相互调换位置即可，对于本例，最终结果即为

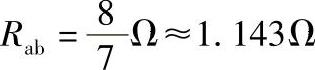
也可用式（1-9）按如下的连续计算法求出：

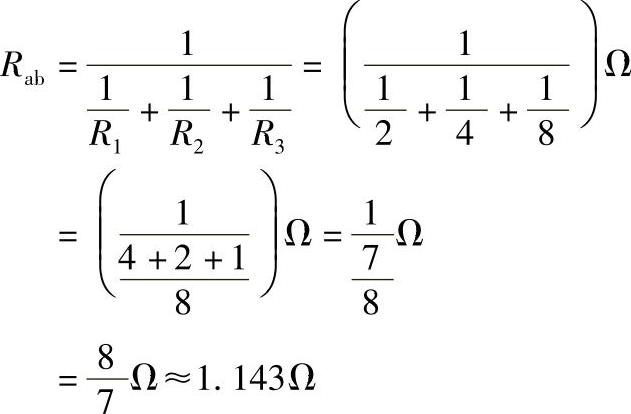
c）本题图中有4个电阻，分成两部分，其中第一部分R₁和R₂串联；第二部分R₃和R₄并联，然后两部分再串联，是一个既有串联又有并联的较复杂电路。R₁=2Ω；R₂=4Ω；R₃=8Ω；R₄=4Ω。

先求出每一部分的电阻：

串联部分为R₁₊₂=R₁+R₂=2Ω+4Ω=6Ω

并联部分为根据口诀“并联只有俩电阻，总阻可用简式求，两阻之积作分子，两阻之和作分母”和式（1-11）可得

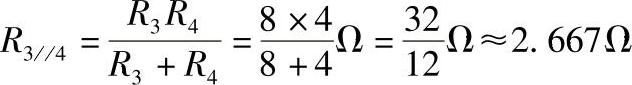
最后按串联的关系求出a、b两端的电阻R_ab（Ω）的数值：

R_ab=R₁₊₂+R₃//4=6Ω+2.667Ω=8.667Ω