（一）口诀

导体阻碍电流流，阻碍能力叫电阻。

导体电阻怎么求？要知截面和长度；

大小与长成正比，与面反比来相求。

不同材料值不同，另外还要看温度。

计算公式用字母，截面S长L；

希文ρ为电阻率，大R小r为电阻。

ρ乘L为分子，截面S做分母。

所用单位要注意，截面米方长度米；

比较复杂电阻率，复合单位欧姆·米。

导体电导符号G，导电能力是其意。

它与电阻呈倒数，单位即为欧分一。

使用字母为S，中文读作西门子。

（二）说明

因为受到字数限制的原因，口诀中将“平方米（m²）”简写为“米方”；“欧姆分之一（1/Ω）”简写为“欧分一”。

1.导体电阻的定义、计算公式和单位

导体对电流的阻碍作用叫做电阻，它是物质的一个物理性质。电阻符号为R或r，基本单位为欧姆（简称“欧”，符号为Ω），另有千欧、毫欧等，符号分别为kΩ和mΩ。

导体的电阻与其长度成正比，与其截面积成反比。即口诀“大小与长成正比，与面反比来相求”。

不同材质的导体对电流的阻碍作用有所不同，在电学中用电阻率（符号为ρ；单位为欧姆·米，符号为Ω·m）来描述导体的这一特性，其有关内容将在本节1.1.2中详细讲述。

导体电阻的大小还与其温度有关，用电阻温度系数来描述导体的这一特性，其有关内容将在本节1.1.3中详细讲述。

用符号代表各物理量，一段材质均匀、截面积处处相同的导体的电阻用下式表示：

(www.daowen.com)

式中 R——导体的电阻（Ω）；

ρ——导体所用材料的电阻率（Ω·m）；

L——导体的长度（m）；

S——导体的截面面积（m²）。

2.关于电导的问题

在一些计算中，有时还要用到电导这一物理量。所谓电导，即导体导通电流的能力。由此可以看出，电导是电阻的反义词。

电导与电阻互成倒数关系，即

式中各量的单位与前面计算电阻的式（1-1）相同，此时电导的单位为“西门子”，符号为S（读作“西门子”）。

西门子是德国一位企业家类型的科学家，是德国西门子（SIEMENS）公司的创始人[全名为维尔纳·冯·西门子，英文为W.Von Siemens，1816—1892]，图1-1所示为其头像。

（三）计算举例

例1：有一条圆铜导线，长100m，横截面积为1.5mm²。求其电阻是多少Ω？

解：本例是已知导体的材质为铜、长度L=100m和截面积S=1.5mm²=1.5×10^-6m²。已知材质即可从相关材料中查到其电阻率ρ（铜的电阻率为1.75×10^-8Ω·m，见表1-1。下同）。图1-1 西门子头像严格地讲，我们所能查到的电阻率都应是温度在20℃时的数值，所以应在计算时明确说明温度的数值，但在一般计算中，如不强调指出此问题，则不考虑它的影响。

按所给出的单位，用式（1-1）计算可求得该段导线的电阻（Ω）为

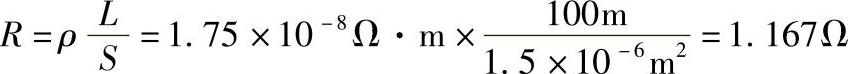
答：这段导线的电阻是1.167Ω。

例2：有一条圆铜导线，长100m，横截面直径为2mm，求其电阻是多少Ω？

解：本例是已知导体的材质为铜，即已知其电阻率ρ，另外知道长度L=100m，但横截面积S没有直接给出，而是给出了截面直径D=2mm=2×10^-3m，这就需要先求出截面积S（m²）的数值后再用式（1-1）求得电阻R的数值（Ω）。

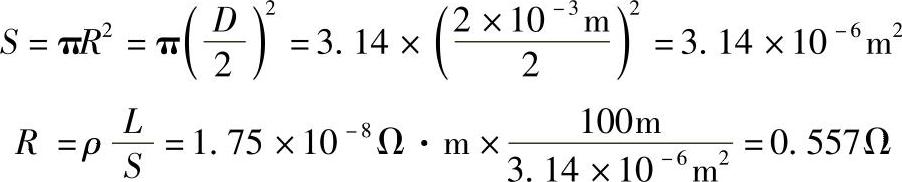
答：这段导线的电阻是0.557Ω。