1896年，物理化学的奠基人Friedrich Wilhelm Ostwald（1853—1932年）首先系统地研究了颗粒粒度对颗粒在液相中的溶解度的影响。他发现小晶粒在液相中溶解，然后在大晶粒表面沉积。这可根据式（10-3）所示的开尔文公式得到解释。将式（10-3）中的蒸气压pr、p分别换为溶解度Sr、S后有以下关系：

式中，Sr为半径为r的颗粒溶解度；S为普通大颗粒的溶解度（在一定温度等条件下，一般为常数）；r为颗粒粒径。由此可见，颗粒小（r小），则其溶解度Sr大，而大颗粒的溶解度小。小颗粒溶解后，通过传质达到大颗粒表面。大颗粒表面处，因溶解度小，物质易达到过饱和而析出，进而使大颗粒变大、粗化。颗粒的这种粗化过程常称为Ostwald熟化（Ostwald Ripening）。1938年，Ostwald的这个发现被用于解释W-Cu-Ni和W-Ni高比重合金的大颗粒生长。

后来，Ostwald熟化或颗粒溶解析出长大成了液相烧结的一种重要机制。这就是我们在10.5.1节提到的溶解-析出过程。1959年，Kingery指出粉末在烧结过程中有少量液相时，固相颗粒的接触区有较高的应力，这种应力使接触区物质的溶解度高于其他地方而首先溶解。然后，溶解的物质扩散到其他溶解度低的区域（如粉末除接触区外的其他地方）而沉积下来，从而使接触面平直化。这可由以下的实验数据得到证实：将直径在200～250μm间的单晶W球（大颗粒）、10μm的W粉（小颗粒）和更细的Ni粉（产生液相）以不同比例均匀混合后，在1670℃松散烧结。结果表明，若烧结过程中，粉末系统出现的液相量适当，没有经过压制的松散粉末仍能获得完全的致密化，同时伴随有小W颗粒的溶解和大W颗粒的生长。而且，液相量较少时，晶粒形状的变化总是从颗粒接触区开始，并发展成平直化的晶界。

1958—1961年，Lifshiz、Slyozov和Wangner将Ostwald提出的小颗粒溶解和大颗粒长大机理引入固体材料中，并用数学模型做理论化处理。粗化后的颗粒尺寸与式（10-70）相似：

式中，K5为常数；R0为初始粗颗粒的尺寸；Rt为t时刻时粗颗粒的尺寸。式（10-93）称为Lifshiz-Slyozov-Wangner方程（简称LSW方程）。许多有液相的烧结系统，其数据与式（10-93）相符。比如UO2-Al2O3有少量共晶液相存在时的烧结、W-Cu-Ni及TiC、HfC、TaC等碳化物以Co作液相时的烧结。

图10.35　纳米Pt在SiO2基底的Ostwald熟化（箭头分别指示了相应粒子的长大和消失）（引自Simonsen，2011）

图10.35为纳米Pt在SiO2基底沉积后于650℃下进行烧结时，在透射电镜下显示的Ostwald熟化。Ostwald熟化不仅出现在有液相的体系中，在固溶体中也存在。在9.6.3节，我们介绍了材料的脱溶沉淀，即第二相（β相）从过饱和固溶体α相中沉淀析出，并在基体α′相中弥散分布。该过程的反应式α—→β+α′。理论上，β相为平衡相。但由于β相的颗粒大小不同而无法达到真正的平衡。

设β相为球形颗粒，则其球形界面使粒子的自由能或化学势升高。球形界面产生的附加压强可由Laplace方程Δp=2γ/r求出。大颗粒（曲率半径r1）和小颗粒（曲率半径r2）之间的化学势可写作：

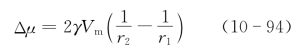
其中γ为界面能，Vm为摩尔体积。以上Δμ正是溶质原子从小颗粒向大颗粒扩散而造成粗化（或Ostwald熟化）的驱动力。通过粗化，界面面积减小，进而界面能下降。大、小颗粒的尺寸相差越大，驱动力也越大。

Ostwald熟化的驱动力还可从浓度的角度来分析。将固溶体系统近似当作稀溶液，则其中某个组元在大颗粒1界面处的化学势μ1为(www.daowen.com)

其中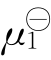为标态化学势，R为摩尔气体常数，c1为组元在颗粒1中的浓度。同样一个组元在另一个小颗粒2界面处的化学势也有与式（10-95）类似的表达式。则该组元在这两个颗粒之间的化学势差为

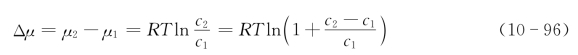
对稀溶液而言，因为（c2-c1）与c1相比很小，故（c2-c1）/c1也很小。我们利用ln（1+x）≈x（x很小）后，式（10-96）可近似为

合并式（10-94）和式（10-97），整理得基体相中小颗粒附近与大颗粒附近的浓度差为

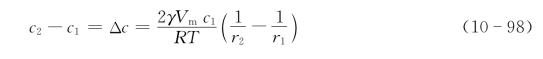
设大颗粒的半径r1→∞，其界面附近的溶质浓度c1=c（∞）；小颗粒的半径r2=r，其界面附近的溶质浓度c2=c（r），则式（10-98）变为

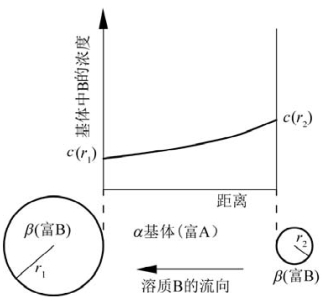
图10.36　不同大小的第二相颗粒β相的Ostwald熟化示意图（这是一个A、B组元构成的二元系统。固溶体α和β分别是富A和富B相。图的上部分示意了随着大颗粒到小颗粒距离的增大，溶质B的浓度变化情况）（引自Mittemeijer，2013）

由上述可见，颗粒半径r越小，其表面附近的溶质浓度或固溶度越大，化学势也升高越多。这种因界面曲率半径减小而引起的自由能升高、溶解度增大，甚至熔点下降等现象称为Gibbs-Thomson效应（Gibbs-Thomson effects）。在纳米级颗粒中，这种效应尤为显著。因此，当过饱和固溶体析出大小不等的第二相（β相）粒子时，由于Gibbs-Thomson效应，在大颗粒β相与小颗粒β相之间的基体中，溶质（B组分）存在一定的浓度梯度。在此浓度梯度的作用下，溶质从β相的小颗粒流向β相的大颗粒。结果，β相小颗粒变得更小，甚至消失。也就是说，较大的β相颗粒通过消耗小颗粒β相而长大，发生粗化，即Ostwald熟化。

图10.36示意了沉淀颗粒之间的溶质浓度变化。在固溶体的脱溶沉淀中，主要是第二相粒子发生粗化，故这种情形中的Ostwald熟化也叫第二相粒子粗化。粗化后的尺寸可用式（10-93）所示的LSW方程得到。

通过对本章及前面章节的学习，读者可能已经了解到烧结、晶粒生长、相变与相平衡对材料显微结构的影响。在9.1.3节，我们介绍了材料的显微结构有晶粒、晶界、相、缺陷（如裂纹、气孔）等。这还不能完全表达显微结构的特征。材料显微结构的特征通常还包括材料所含空隙的大小、数目；每一个晶粒的相对数量、大小、形状和取向。前面章节未涉及晶粒取向。若材料中的晶粒取向具有一定的规律性或择优分布，则构成显微结构的一种特殊形式——织构。