除了晶界曲率引起的化学势梯度导致晶界移动外，晶界迁移率B对晶界的移动速率同样有影响［见式（10-60）］，因而影响晶界迁移率的因素也将影响晶界的移动，这些因素有晶界的曲率、温度、第二相粒子、气孔等。

1.晶界的曲率。这方面的影响不再赘述。

2.温度

温度对晶界迁移率B的影响主要是通过影响晶界扩散系数DB来实现的。B与DB有如下关系：

而DB又可表示为

其中D0为指前因子，Ea为活化能。综合以上两式，得

式（10-67）中，指数项的影响大于1/T，故温度升高，晶界迁移率增大。既然晶界的移动导致晶粒的生长，那么温度对晶粒尺寸就有直接的影响。

式（10-64）表示了晶界移动速率v2：

v2与晶界的曲率半径r成反比，即小晶粒的曲率半径r小，晶界移动速率大；晶粒尺寸大，晶界移动速率小。设dt时间内，晶粒平均半径R的变化为dR，则dR/dt可表示较大晶粒平均半径的长大速率。由于晶界的移动速率v2大，较大晶粒生长也快，故可用晶界移动速率表示较大晶粒平均半径的长大速率：

用晶粒平均半径R代替上式中的晶界的曲率半径r，Vm、γ、λ为常数。在一定的温度下，由式（10-67）我们可知B也为常数。将这些常数合并到新常数K1中，整理后得

积分式（10-69）得

其中K2为积分后获得的常数，Rt为经时间t后的平均晶粒半径，R0为恒温下的起始晶粒平均半径。

我们在前面把晶界迁移率B当成常数，而将其合并到式（10-70）中的常数项K2中。若把含温度的指数项列出（1/T的影响较指数项小而合并到常数项中），则积分后有

其中K3为另一常数。对特定材料而言，起始晶粒平均半径R0往往是定值，故可反映晶粒尺寸的长大情况。这样，式（10-71）就能粗略地表示晶粒的平均尺寸Rt随温度呈指数增大。

在晶粒生长到后期，Rt≫R0，故式（10-70）变为

其中K4=。式（10-72）为晶粒正常生长的经典抛物线方程，它表明晶粒的平均尺寸随保温时间的1/2次方增大。这符合一些实验结果。结合式（10-71），可得出结论：在影响晶粒长大方面，升温比延长保温时间有更显著的影响。

但一些氧化物（Al2O3、UO2）的晶粒生长表明，式（10-72）中时间t的指数处于1/3～1/2之间，且接近1/3的情况居多。这主要是由于晶界在移动过程中会受到第二相粒子、气孔等的阻碍，故式（10-71）和式（10-72）的一般表达式为

其中n=2或n=3。

3.第二相粒子

当一个晶界在运动中遇到第二相时，第二相质点对晶界产生一定的阻力而拖住晶界。这导致晶界的运动减缓，甚至使晶界停止运动。

设第二相质点为球形粒子。如图10.26（a）所示，当晶界在下半球面与球形粒子相遇时，随着晶界往上移动，晶界面积A减小，晶界能γA降低。晶界上升到球心位置时，面积减少πr2，晶界能减少γπr2。此时晶界能最小，粒子与晶界处于力学平衡态。若晶界继续往上移动，则晶界面积增大，晶界能增加。在晶界表面张力的作用下，晶界发生弯曲，以尽可能使晶界与粒子表面相垂直。晶界表面张力对晶界的作用力F可表示为

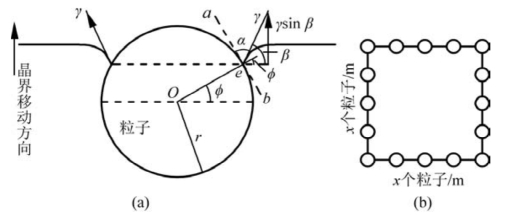
图10.26　（a）球状第二相粒子与晶界作用示意图（引自徐祖耀，1986）；（b）单位面积上粒子分布的示意图，只表示出了每边的粒子数，面积中部未示出原子

为使读者明白拉力的计算，我们将各物理量的单位表示在公式的括号中。l为晶界与第二相粒子接触的周长。

当晶界处于图10.26（a）所示位置时，粒子与晶界接触的周长l=2πrcosφ。在晶界运动方向上，晶界表面张力γ对粒子施加的拉力F为γ沿晶界运动方向的分力γsinβ。故晶界沿其运动方向对粒子的拉力为

根据作用力与反作用力的原理，晶界对粒子的拉力也是粒子对晶界运动的阻力。结合图10.26（a）中所示关系，ab与oe线相垂直，故β=90°+φ-α。再利用三角关系整理sinβ，则第二相粒子对晶界的阻力可进一步表示为

一定条件下，给定材料的晶界表面张力γ是定值。那在什么情况下，第二相粒子对晶界的阻力达到极大值呢？这实际是在问晶界在何处或φ为何值时，阻力F具有极大值。因此，将F对φ求导：

再用三角函数的转换关系整理后得

dF/dφ=0时可求得使F获得极大值的φ，即sin（α-2φ）=0，α-2φ=0。因此，当φ=α/2时，第二相粒子对晶界的阻力达到极大值。将φ=α/2代入式（10-77）得到此时的阻力极大值为(www.daowen.com)

式（10-80）表示了一个第二相粒子对晶界的阻力极大值。若有多个粒子，其阻力极大值又是多少呢？

因晶界是一个二维面，故假设单位晶界面积上的粒子数为ns，则这些粒子在单位面积上对晶界的总阻力为

下面我们求ns。再假设粒子是均匀分布的，单位长度上有x个粒子，即x（个/m），如图10.26（b）所示，则单位面积上的粒子个数为x2个，即ns=x2。假设每个粒子是球形，其半径为r（m），直径为2r（m）（括号内为单位）。也就是一个粒子在晶界面上占据的长度为2r（m/个）。该粒子直径的倒数1/2r（个/m）实际就为单位长度上的粒子数x，则

这样看来，单位体积的多晶材料中，第二相粒子的个数nV就为x3个。

将式（10-82）代入式（10-83）得

有了ns，但nV又不知道，也不容易在实际中操作，故将nV转化为容易操作的体积分数。nV个第二相粒子在单位体积（V=1）多晶材料中所占的体积分数f为

由式（10-85）得出

将式（10-86）代入式（10-84）：

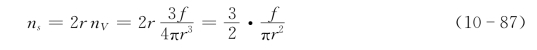
将式（10-87）代入式（10-81）求出单位面积上，第二相粒子对晶界的阻力：

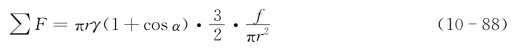
化简得晶界受到的阻力：

这里的∑F是单位晶界面积上，晶界受到的阻力，而单位面积上的力为压强（或应力）。因此，应力∑F是第二相粒子对晶界的阻力。

而晶界还有驱动力。晶界曲率引起晶界的移动，而且是向晶界的曲率中心方向移动。如图10.23所示，单位晶界面上晶界的驱动力实际为曲率引起的附加压强2γ/R*。R*为晶界曲率半径，若晶粒是球形，则R*为晶粒半径。在此，我们假设多晶材料中的晶粒为球形，故R*为基体晶粒尺寸。当晶界的驱动力和阻力相等而达到平衡时2γ/R*=∑F，晶界停止运动，此时晶粒达到稳定尺寸R：

整理式（10-90）后得

图10.26中，若α在晶界运动过程中保持不变，则式（1091）又可写为

式（10-91）和式（10-92）表明晶粒长大的极限尺寸R与第二相粒子的大小r成正比，与其体积分数f成反比。第二相粒子小、数量多，则晶界受到的阻力大、晶粒的稳定尺寸R小，晶粒细。正因如此，在陶瓷材料和粉末冶金制品中往往加入第二相物质作为晶粒长大抑制剂。比如在WC-Co金属陶瓷材料的烧结中，人们常引入VC或Cr2C3来抑制WC晶粒的长大。由于获得了细晶组织，材料的强度得到了提高，因此，在烧结中引入第二相可使材料得到强化。这与我们在上一章提到的从过饱和材料中析出沉淀颗粒、阻止位错移动来强化材料一样，都属于第二相强化。若第二相是从过饱和材料沉淀析出则常称为析出硬化、沉淀强化或时效硬化；若第二相是人为加入的（比如粉末烧结时加入）则常称为弥散强化。

4.气孔

与第二相粒子相似，气孔对晶界也有一定的影响。比如，气孔也能钉住晶界，从而抑制晶粒生长。若晶界的驱动力大于气孔对晶界的阻力，则晶界有可能脱离气孔而继续前进，也有可能晶界拖着气孔一起前进。在气孔与晶界一起前进的过程中，原子可通过界面扩散、表面扩散、体积扩散或黏滞流动、溶解-沉淀及蒸发-凝聚机制传质。这里，我们用vP表示气孔的迁移速率。气孔随晶界移动并逐渐集中到界面交接处，并随着晶粒长大而聚集成较大空隙，如图10.27所示。

图10.27　UO2在1600℃时的晶粒长大和气孔长大（引自Kingery，2010）

（a）处理2 min后的情形，相对密度91.5%；（b）处理5 h后的情形，相对密度91.9%（黑色斑块为气孔，它们几乎都在多个晶粒交汇的角落处）

在粉末烧结过程中，晶界与气孔的移动速率对烧结体的致密化有重要影响。烧结初期，气孔的体积分数大而抑制了晶界的移动。在此阶段，晶界的移动速率v2≈0，如图10.28（a）所示。由于晶界结构疏松，原子以晶界为快速扩散通道作扩散传质。聚集于晶界处的气孔利用晶界完成汇集和排气，结果气孔率下降，粉末坯体的致密化程度提高。

到了烧结中、后期，坯体中的气孔率下降。这时，可以出现晶界的移动速率v2与气孔移动速率vP相等即v2=vP，如图10.28（b）所示。当这两个速率相等时，气孔仍与晶界结合在一起。因而，气孔也容易通过晶界达到排除。此时，应适当保温，以进一步降低气孔率。但是，若再继续升高温度，就很容易导致v2＞vP。这是由于晶界的移动速率v2是随温度呈指数增大的，见式（10-67）。在此情况下，晶界很快脱离气孔向曲率中心方向移动，气孔则留在长大了的晶体中，如图10.28（c）所示。这种气孔只能通过体积扩散来加以排除，而体积扩散系数比晶界扩散系数小得多，故留在晶体中的气孔很难得到排除。图10.25显示了正常长大的多晶CaF2晶体中有明显的气孔存在。这种现象也可以发生在粉末的烧结初期。比如，粉末中非常细小的晶粒，其曲率半径小，晶界移动快，从而容易将气孔留在个别较大晶粒中。因此，在粉末制品的烧结过程中，常采用控制温度、晶粒大小等措施来尽量避免将气孔留在晶体中。

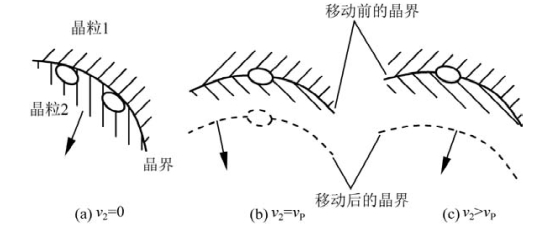
图10.28　晶界遇到气孔时的情况（箭头所示为晶界移动方向，空心椭圆形球代表气孔）（引自陆佩文，1991）

5.杂质、溶质原子和液相

微量的杂质、固溶原子往往富集于晶界附近形成“气团”。晶界移动时将拖着“气团”一起运动。若杂质、固溶原子的扩散较慢，则会对晶界的运动产生阻碍，甚至脱离晶界。这些物质与晶界的作用类似于晶界与第二相颗粒或气孔的作用。

此外，晶界处有少量液相时，两个新的固液界面会形成。这种界面的形成会降低晶界能量，进而降低晶界移动的驱动力、使晶界生长得到抑制。但液相过多时，原子的扩散传质容易，这反而促进晶粒生长，如下文的Ostwald熟化。

6.相邻晶粒的取向差

晶粒间的取向差主要影响晶界的结构。取向差大，晶界处的结构比较疏松，原子的扩散系数大。取向差小（如小角度晶界）说明晶界两侧的晶粒在晶界处结合得较好，晶界结构较致密。特别地，取向差为零时，晶界消失。原子在取向差为零之处的扩散实际上是晶格扩散。因此，小角度晶界的迁移率要低于大角度晶界的迁移率。

晶界结构不同，杂质和溶质原子在晶界的吸附成“气团”的能力也不同。无杂质和溶质原子时，如上文所述，大角度晶界的迁移率大。但大角度晶界又容易吸附杂质和溶质原子，故有杂质存在时，大角度晶界的迁移率通常要下降。

总之，晶界移动导致晶粒长大。影响晶界移动的因素都会影响晶粒的生长。在了解了晶粒生长的基本情况后，还有一个重要问题未解决：究竟什么是晶粒生长？再结晶也是晶界移动的结果。晶粒生长与再结晶有何不同？