当Frenkel提出黏性流动的两液滴模型后，Reginald Nunes Nabarro（1916—2006年）认为单个空位不能在单一的应力（如只有拉应力）下运动。1948年，Nabarro建立了空位在拉应力-压应力下运动的扩散蠕变模型。

1.体积扩散蠕变

Nabarro指出，多晶材料在剪应力作用下可通过自扩散而变形或屈服。这种变形使多晶材料产生像黏性流体一样的宏观行为。这是由于在剪切应力作用下，多晶材料中受压应力的晶界与受拉应力的晶界之间同时存在浓度梯度和应力梯度，故原子（或空位）产生定向扩散流动。原子从受压应力的晶界处先向晶粒内部扩散，然后再向受拉应力的晶界处扩散，可见体积扩散蠕变传质是整排原子沿应力方向的移动。这种传质在高温、低应力下是可能发生的。它与前文叙述的扩散传质不同，单纯的扩散传质仅仅针对单个质点的迁移。

1950年，Conyers Herring（1914—2009年）以图10.14为例计算了应力-应变关系，并认为多晶材料具有“扩散黏度”。描述这种体积扩散的蠕变方程称为Nabarro-Herring方程，即

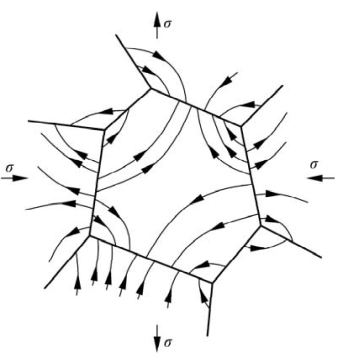
图10.14　应力作用下，多晶体晶界上的原子自扩散流（粗实线表示晶界；细实线及箭头表示扩散方向；σ为宏观应力）（引自Herring，1950）

式中，ε为均匀剪切应变速率，或称作黏性蠕变速率；D*为自扩散系数；Ω为原子体积；G为晶粒尺寸；σ为平均宏观应力。Herring还得到多晶材料的宏观“扩散黏度”η：

式（10-54）和式（10-55）表明，晶粒尺寸G大，原子扩散路径长，则晶体的扩散黏度η大，蠕变速率ε低。因此，黏性蠕变传质常常局限于如晶界、位错等局部区域，尤其是在无外力作用时更是如此。(www.daowen.com)

2.晶界扩散蠕变

多晶材料有许多晶界。高温下，晶界黏度会迅速下降。此时，应力使晶界产生黏滞流动，而且晶界处的空位扩散和位错攀移也比晶粒内部更容易（见4.4.6节）。因此，晶界对蠕变有重要影响。1963年，Coble提出：原子的晶界扩散系数大于体积扩散系数。若原子在晶界的扩散影响材料的形变，则晶界扩散可能会控制材料的蠕变速率。他以多晶Al2O3为例，得处了晶界扩散控制的蠕变方程：

式中，DB为晶界扩散系数；w为晶界宽度。其余符号意义同式（10-54）。这种由晶界扩散控制的蠕变被称为Coble蠕变，其蠕变速率ε与应力σ的一次方成正比。而式（10-54）描述的Nabarro-Herring蠕变主要发生在晶粒内部，即晶格蠕变。

对比式（10-54）和式（10-56），我们可知Nabarro-Herring蠕变速率ε∝1/G2，Coble蠕变速率ε∝1/G3，故Coble蠕变比Nabarro-Herring蠕变对晶粒尺寸G的依赖性更大。这两类蠕变大多发生在高温及应力低于10 MPa，或中低温低应力环境中。

除了Nabarro-Herring蠕变外，晶格蠕变还有位错滑移蠕变。这种蠕变的速率受位错间空位扩散机制的控制，而刃位错通过攀移会使空位消失，故位错滑移蠕变主要发生在中高温且承受10～1000 MPa拉应力的材料中。

在学习本节时，读者可能有这样一个疑问：蠕变与粉末烧结有什么关系呢？把蠕变和烧结联系起来的主要原因是科学家们发现金属粉末的加压烧结过程与金属的蠕变过程极为相似。而且，粉末体在烧结过程中，原来粉末间的固气界面逐渐被晶界所取代（图10.1）。如前所述，晶界和晶格扩散在蠕变过程中有很重要的影响。因此，将蠕变理论引入烧结过程的研究中是可行的。

当粉末坯体在一定温度下受到外压作用时，坯体内会产生一定的应力分布。而且，这些应力在坯体中的分布是不均匀的。由于应力集中现象，在孔洞处的应力较大，特别是在烧结初期，外部压力通过颗粒接触点进行传递。此时，接触点的应力在理论上可趋于无穷大。随着烧结的进行，粉末间的接触面积增大，此处应力逐渐下降。在这些应力及高温的作用下，粉末坯体以晶界蠕变和晶格蠕变的传质形式使原子产生迁移消除气孔而达到致密化。如今，烧结蠕变已成为粉末物质的一种重要传质机制。

至此，我们介绍了烧结的两种基本理论（扩散理论和流动理论）。它们是所有粉末烧结理论的基础。利用这些理论作指导，人们可采取一些措施控制粉末的烧结过程。但在实际生产中，往往不是单一机制控制整个烧结过程。有时是其中某种机制起主要作用，有时是多种传质机制共同作用。比如，有液相出现的烧结，初期流动传质是主要的，后期扩散传质变得重要。此外，烧结条件改变，传质机制也会改变。因而，这些烧结基本理论虽然能对材料的烧结提供一定的指导，但很多时候仍满足不了某些新型材料低温、快速烧结的需求。为此，人们提出了强化烧结的概念。