可用黏性流动机制描述的系统有：剪切应力作用下的高温玻璃相、热压烧结过程中的粉末。此外，高温下依靠黏性液体的流动来达到致密化的液相烧结也可用黏性流动来讨论。

从扩散机制来看，由液体或固体的黏性流动引起的烧结是由空穴或空位的扩散引起的。于是，Frenkel用非晶态物质的黏性流动来解释这种空位的运动。而且他还强调，晶体的黏性流动机制和晶体在滑移面上的塑性变形机制不同。黏性流动是一慢过程、一个空位在应力（如毛细管力）作用下的运动，且这种运动和扩散有关；而塑性变形是一快过程、一个不需要热激活的最终变形。

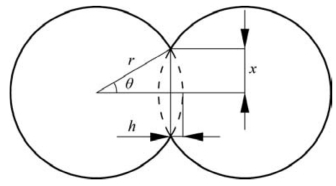
图10.12　Frenkel两液滴“黏结”模型（引自果世驹，1998）

接着，Frenkel将粉末简化为球形。然后，他用球形液滴的对心运动模拟了粉末颗粒的黏结过程，进而得出粉末在黏性流动机制下的颈长方程。Kuczynski称Frenkel的这项研究为第一个烧结科学方面的理论工作。图10.12为Frenkel两液滴模型。开始时，单位时间内，表面张力γ作用于一个液滴表面所做的功为

其中r0为液滴的起始半径。与此同时，物质的流动因黏性而受到内摩擦力的阻碍。单位时间内，该内摩擦力所做的功为

式中，η为物质黏度；δ为速度梯度。

表面张力γ作用于液滴表面所做的功W1与流体因黏性流动造成的能量消耗速率W2相等：

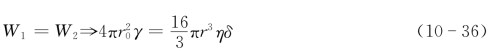
通常r≠r0。但在黏结初期，靠近的距离小，故近似认为r=r0，则式（10-36）变为

下面我们求速度梯度δ。图10.12中，dt时间内，两液滴靠近的距离h可表示为

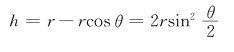
θ很小时，sin（θ/2）≈θ/2，故

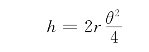
沿球的径向方向，单位径向长度上的速度变化，即速度梯度为dv/r，因为在dt时间内，靠近的距离为h，故dv=dh/dt，因此速度梯度δ为

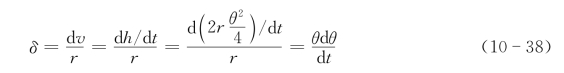
将式（10-38）代入式（10-37）得

积分得

若γ、r和η与时间无关，则积分得

由图10.12所示模型可知，两液滴间的接触面积πx2=π（rsinθ）2。同样，当θ很小时，sinθ≈θ，故πx2=πr2θ2。由此得到(www.daowen.com)

合并式（10-41）和式（10-42）得

开方得

式（10-44）是不是与前文介绍的扩散传质机制的颈长方程类似，只是r和t的指数不同？式（10-44）表明黏性流动机制引起的粉末接触颈生长也与粉末颗粒尺寸r和烧结时间t有关。由于接触颈生长与时间的1/2次方成正比，故与上节的扩散机制相比，黏性流动机制引起的接触颈生长较快、致密化速率较大。除此以外，粉末接触颈生长还受物料表面张力γ和黏度η的影响。

黏性流动引起粉末接触颈生长的同时，还使粉末颗粒的中心靠近而产生收缩。由此引起的收缩率为

式（10-45）表明粉末体的收缩率与表面张力成正比，而与黏度和颗粒尺寸成反比。

式（10-44）和式（10-45）主要描述粉末在黏性流动初期的情形。随着烧结的进行，原来连通的气孔会缩小为孤立封闭气孔。根据Laplace方程，每一个球形气孔有一个指向气孔曲率中心的附加压强，其大小为-2γ/r。这相当于有一个大小为-2γ/r的压强作用于气孔使其缩小而达到致密化。具有大小相等孤立气孔的黏性流动坯体，其收缩速率可表示为

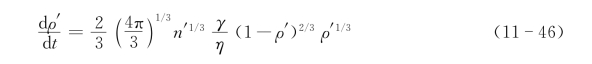
式中，ρ′为相对密度；n′为单位体积无孔固体中的气孔数。

如何理解n′的意义呢？假设一个体积为V的实际物体。我们将其想象成两部分：气孔体积V′、完全致密的无孔固体，体积为V″，则V=V′+V″。这就相当于V″体积的无孔固体具有V′体积的气孔，故单位体积无孔固体所含气孔体积可表示为V′/V″。若单位无孔固体含有的气孔数为n′，一个气孔的体积为4πr′3/3，r′为气孔半径，则单位体积无孔固体中的所有气孔体积就为n′4πr′3/3，即：

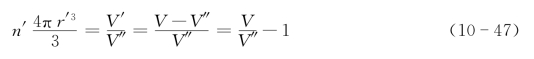
设这个体积为V的实际物体质量为m。因气孔质量可忽略，故m实际上也是其中无孔固体的质量。由密度定义式，实际物体的V=m/ρ（ρ为含有气孔的物体密度）。同理，无孔固体的体积V″=m/ρ0（ρ0为不含气孔的物体密度，即理论密度）。将V、V″的表达式代入式（10-47）得

根据式（10-2），式（10-48）可改写为

将式（10-49）整理成n′1/3的表达式：

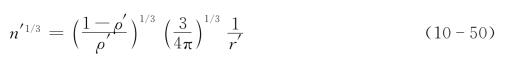
将式（10-50）代入式（10-46），得

若做近似考虑，气孔尺寸r′与颗粒起始半径r0的关系为r′≈0.41r0，则式（1051）变为

式（10-52）表明颗粒起始半径r0小，黏度小，表面张力大，则致密化速率大。

图10.13表示了粉末在高温下形成黏性硅酸盐液体时相对密度随时间的变化情况。同样的时间，温度高，则液体的黏度低而容易流动以填充粉末间的空隙，故致密化速度大。从图10.13可看出实验值与实线非常吻合，这说明式（10-46）或式（10-52）可用于描述黏性流动的致密化过程。