1.应力作用下的空位摩尔分数

图10.8为粉末烧结的双球模型。接触颈凹面为固-气界面。由于界面张力γsv的作用，颈部受到的合力γ1为张力，其方向如图10.8所示。该张力产生的应力（即压强）为张应力。张应力使双球中心距缩小。在张应力的作用下，双球接触面产生静压力F2，F2在接触面的应力为压应力。压应力促使物质的定向迁移，即物质向空位处扩散，或者说空位向物质扩散。

在压应力区（双球模型的接触面处），一个空位的形成能Ev可表示为Ev=E0+σΩ，其中E0为无应力时的空位形成能，Ω为扩散空位处的原子体积。张应力区（接触颈处）的空位形成能Ev=E0-σΩ。其中+σ表示压应力，-σ表示张应力。

无应力区，空位的摩尔分数为

式中，n为晶体中的空位数；N为晶体中的原子总数；kB为玻耳兹曼常数；T为热力学温度。据此，在压应力区（如双球接触面处），空位的摩尔分数Ce可表示为：Ce=。将Ev=E0+σΩ代入，整理后得

因为σΩ/（kBT）≪1，有exp［-σΩ/（kBT）］≈1-σΩ/（kBT），所以式（10-11）可简化为

同理，在张应力σ作用时，用Ev=E0-σΩ取代式（10-10）中的E0，则在张应力区，空位的摩尔分数Ct为

由式（10-12）和式（10-13），接触颈（张应力区）和接触面（压应力区）之间的空位摩尔分数之差为

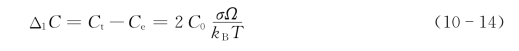
接触颈（张应力区）与颗粒中心（无应力区）之间的空位摩尔分数之差为

以上计算得出Ct＞C0＞Ce，Δ1C＞Δ2C，这表明粉末颗粒不同受力部位的空位摩尔分数不同。接触颈部的张应力区空位摩尔分数大于无应力区的。而在接触面的压应力区，空位摩尔分数最小，故空位容易首先从接触颈向接触面处扩散，其次才从颈部向颗粒中心扩散。这种空位扩散也是原子等物质的反向扩散，即原子容易首先从接触面向接触颈扩散，其次才从颗粒中心向颈部扩散。图10.9示意了烧结初期可能的原子扩散路径。

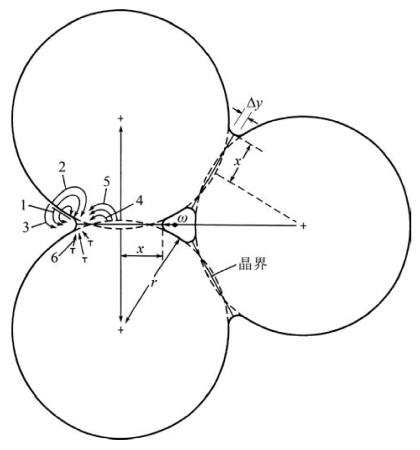
图10.9　烧结初期可能的原子扩散路径（引自Kingery，2010）

1—表面扩散（表面至颈部）；2—晶格扩散（表面至颈部）；3—气相传质（表面至颈部）；4—晶界扩散（晶界至颈部）；5—晶格扩散（晶界至颈部）；6—晶格扩散（位错至颈部）

2.烧结初期的颈部增长动力学方程

以图10.9中机理5—晶格扩散（晶界至颈部）为例。原子首先向无应力颗粒中心扩散，再向接触颈扩散。该过程的动力学计算方法与蒸发-凝聚一样，即表面物质的迁出速率等于使物质体积增长的迁入速率。但与蒸发-凝聚模型不同，此时采用图10.5（c）模型。该模型的接触颈曲率半径ω、颈部面积A及颈部体积V分别为

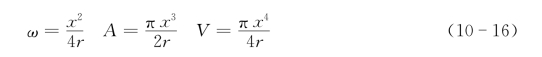
因为原子首先向无应力颗粒中心扩散，所以应采用式（10-15）表示的接触颈部与颗粒中心（无应力区）之间的空位摩尔分数之差为Δ2C。张应力σ（N/m2）可表示为

上式括号内为单位，故Δ2C可表示为

在此空位摩尔分数差的条件下，设空位在单位时间内、沿颈部圆周单位长度向晶界扩散的量为J（个·s-1·cm-1），J=4DvΔC，其中Dv为空位扩散系数，若D*为自扩散系数，则Dv=D*/（ΩC0）。

根据图10.5（c），接触颈周长为2πx。因此，单位时间内从接触颈部传出的空位体积为

将J=4DvΔC和Dv=D*/（ΩC0）代入式（10-18），并用式（10-17）取代J中的ΔC，得

将dV=Adx和式（10-16）中的A、ω代入式（1019），整理后有

对式（10-20）进行积分

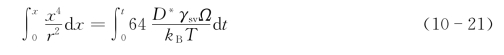(www.daowen.com)

得

在式（10-22）两边同乘以1/r3，得

将式（10-23）两边同时开方得

式（10-24）为烧结前期，由晶格扩散控制的接触颈之长大速率方程。它的变化趋势与式（10-9）所示蒸发-凝聚控制的颈部长大速率相似，而且其颈部长大曲线的图形也与图10.7类似，即接触颈在烧结初期增长较快，后期较慢，但扩散控制的接触颈生长时有收缩现象。

实际上，在应用式（10-24）的过程中，测定x/r比较困难，故常用粉末体的体积收缩率或线收缩率来代替。设两颗粒原来的中心距为L0，中心缩短的距离ΔL（或原来的粉末体体积V0，收缩后的体积减小量ΔV），结果有：

美国陶瓷学家Robert L.Coble详细研究了Al2O3的烧结，结果表明x/r、ΔL/L与时间的关系分别符合式（10-24）和式（10-25）。根据图10.9，扩散机制除了5所示的晶格扩散（或体积扩散），其他机制也可导出与式（10-24）类似的关系。比如：表面扩散机制，颈部增长的速率有以下关系：

晶界扩散机制，颈部增长的速率关系为

虽然文献表明，不同人推导出的速率方程略有差异，但x/r随起始粒径r和时间t的变化趋势还是一致的。因此，扩散控制的颈部增长动力学方程（包括蒸发-凝聚机制）可统一写为

其中F（T）表示与温度的函数关系。

以上这些颈部增长的速率方程主要适用于烧结初期。在这一时期，原子等质点从粉末颗粒的表面、晶格和晶界等位置向接触颈扩散。其间，颗粒发生重排、空位扩散至晶界等处而消失。在此过程中，颈部体积的增长速率与扩散传质的速率相等。虽然这些扩散传质机制比较符合许多粉末在初期烧结的情况，但它们引起的颗粒和空隙形状的变化较小、收缩也小（线收缩率ΔL/L＜0.06）。当颈部增长x/r≈0.3时，人们通常认为烧结中期开始了。

3.烧结中期的动力学方程

经过烧结初期的发展，原来的球形颗粒逐渐变成多面体。为此，Robert L.Coble于1961年提出了著名的简单连通孔模型。

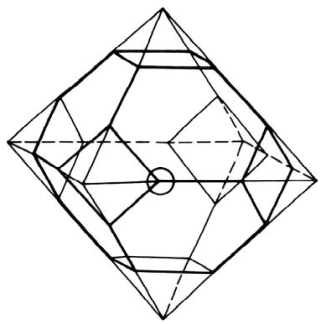
图10.10　十四面体单颗粒及简单孔洞模型（引自果世驹，1998）

Coble假定烧结体由十四面体和孔洞堆积而成。这种十四面体实际为一个截角八面体（即八面体的六个顶点分别被一平面所截），如图10.10所示。十四面体的每一条棱边由三个颗粒共有。图中的粗线表示简单的圆柱形孔洞。这些孔洞相互连通，而且是空位源。图中的圆表示烧结末期的封闭孔洞。据此模型，Coble得到孔洞的体积分数f（即空隙率）与烧结时间的关系为

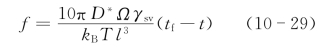
式中，l为圆柱形孔洞的长度；tf为孔洞完全消除所需时间；其余符号的意义同前。式（10-29）为简单连通孔洞模型中，体积扩散机制引起的烧结中期致密化动力学方程。Coble指出式（10-29）适用于孔洞没有完全消失或晶粒生长还未开始，孔洞呈连通状的情形。

若在烧结初期，晶界扩散起主要作用，则空隙率f的表达式为

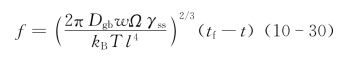
式中，w为晶界宽度；Dgb为空位在晶界的扩散系数；γss为晶界能。式（10-29）和式（10-30）表明：无论是体积扩散，还是晶界扩散机制起主导作用，粉末体在烧结中期的孔洞体积分数f与时间t都呈一次方线性关系，也即空隙率随烧结时间而线性地减少，故致密化速率较大。

烧结中期的特点主要有：颈部进一步扩大、颗粒变形大；气孔由不规则形状逐渐变成由三个颗粒包围的近似圆柱形气孔，且气孔间相互连通；致密化程度比烧结初期显著，收缩率达80%～90%，坯体气孔率降低到50%左右；晶界开始移动而导致晶粒生长。这一时期，传质机制主要是原子以晶格扩散和晶界扩散的方式向气孔迁移。随着烧结的进行，孔洞的体积分数f减小，而且原来连通的孔洞开始分开呈不连通状。此时，烧结进入后期。

4.烧结后期动力学方程

图10.10中，粗线表示简单的圆柱形孔洞分别向十四面体的顶点退缩，直至分开呈孤立、不连通状，进入烧结末期。图10.10用小圆示意了一个封闭孔洞。其实，十四面体的24个顶点都有一个这样的封闭气孔，且形状近似球形。据此，Coble得出烧结后期，孔洞的体积分数fs（即空隙率）与烧结时间的关系为

式（10-31）表明粉末体在烧结后期的孔洞体积分数fs与时间t也呈线性关系。这说明烧结中、后期的致密化无显著差异。Al2O3的相对密度在低于95%的理论密度时，坯体的相对密度与时间近似呈直线关系，这表明式（10-31）在一定范围内的正确性。若烧结时间继续延长，封闭气孔率并不会进一步减小，甚至为零。相反，若烧结时间过长，烧结体中的晶粒会出现生长过大等削弱材料某些性能的现象。这方面的问题，我们将在后文介绍。

烧结后期的特点：气孔完全孤立而呈近似球状；质点主要通过晶界扩散和体积扩散进入气孔，而达到致密化；坯体收缩率达90%以上，相对密度也在理论值的95%以上；与前一阶段相比，晶粒明显长大；烧结体的强度得到提高。

蒸发-凝聚和扩散传质机制主要针对纯固相粉末烧结中的传质。在此传质过程中，物质没有受到外部施加的应力作用，而且也无液相的出现。若粉末坯体在烧结时，受到外部应力，或出现少量液相，则烧结过程的传质机制可以用流动理论来描述。