根据开尔文公式：

式中，pr是半径为r的液滴或气泡的蒸气压；p为平液面的蒸气压；γ为液体表面张力；M为液体相对分子质量；ρ″为液体密度；R为摩尔气体常数；T为热力学温度。凸液面的r＞0，pr＞p，即液滴等凸液面的饱和蒸气压大于平液面的饱和蒸气压；凹液面的r＜0，pr＜p，即凹液面（如气泡）的饱和蒸气压小于平液面的饱和蒸气压。因此，毛细管内的蒸气容易凝聚成液体。虽然以上情形针对的是液体，但开尔文公式对固体，尤其是高温下容易挥发的物质，如PbO、BeO仍然适用。

图10.5中，接触颈为凹面，其曲率半径ω为负；其他部位为凸面，曲率半径r为正。颈部凹面处的蒸气压p1用开尔文公式表示为

式中，p0为平表面蒸气压；γsv为粉末的表面能；ρ‴为密度；其余符号的意义同前。

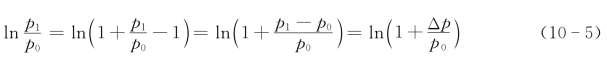
根据数学知识，当x很小时，ln（1+x）≈x。在式（10-5）中，压差Δp很小，故ln（p1/p0）≈Δp/p0。又因为接触颈半径x≫ω，所以式（10-4）可简化为

式（10-6）表明Δp=p1-p0＜0，即原子在接触颈凹面处的蒸气压小于平表面的平衡蒸气压。同理也可得出，原子在接触颈凸面处的蒸气压大于平表面的平衡蒸气压，故原子在粉末颗粒凸表面处蒸发，而在凹面处凝聚，从而使颈部逐渐被填充，如图10.6所示。

凸面原子蒸发产生的气态物质在凹面凝聚，该情形可近似地用固体对气体吸附的Langmuir方程描述。这样可得出气态物质在单位时间、单位面积上的凝聚速率v与压差Δp的关系：

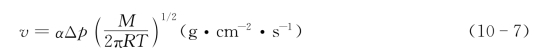
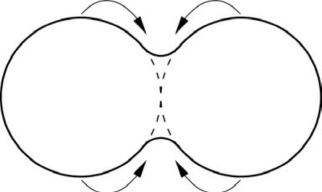
图10.6　蒸发-凝聚起始阶段示意图（引自Kingery，2010）(www.daowen.com)

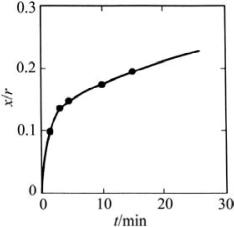
图10.7　725℃时，NaCl球形颗粒颈部长大曲线（引自Kingery，2010）

其中α为调节系数，α≈1。单位时间内，物质在颈部的凝聚量等于颈部物质体积的增加速率时，有：

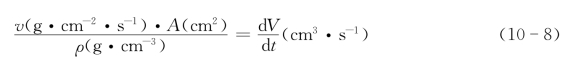
为使读者清楚式（10-8）的意义，我们引入了各量的单位，并将单位置于括号内。

图10.5（b）中，x/r＜0.3时，接触颈半径ω≈x2/（2r），接触颈透镜（图10.6中虚线所示）表面积约为A=π2x3/r，接触颈体积约为V=πx4/2r。将这些近似值及式（10-6）和式（10-7）代入式（10-8），整理、积分后得

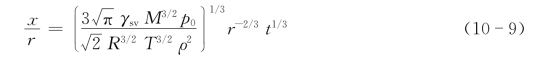
上式是Kingery等用双球模型推出的。它表明了颗粒间接触面的半径和影响其生长速率的变量（r，t，p0）之间的关系。若把式（10-9）中的括号部分和r看作是常数的话，则接触颈的生长x/r随时间t的变化如图10.7所示。

图10.7表明粉末接触颈在烧结初期增长较快。随着烧结时间的延长，接触颈的增长逐渐减缓，而延长烧结还会带来后续晶粒生长等问题。因此，企图采用无限延长时间来促进致密化是不可取的。式（10-9）还表明，粉末起始粒径r小，则接触颈增长快，这可促进粉末的致密化。而粉末起始粒径r和烧结时间t是两个在粉末体烧结时容易控制的参数。

采用蒸发-凝聚传质时，原子从粉末凸面蒸发，在凹面处凝聚。在此过程中，粉末颗粒的中心距并未受到蒸发-凝聚传质的影响，即烧结时，粉末坯体不产生收缩。NaCl在750℃烧结时没有发生收缩表明了蒸发-凝聚具有一定的合理性。

蒸发-凝聚需要物质具有可观的蒸气压。对微米级颗粒而言，蒸气压的数量级要大于1.01～10.13 Pa。然而，大多数氧化物、金属和硅酸盐等固体物质在高温下的蒸气压都低于这个值。因此，这些蒸气压很低的粉末，其烧结致密化主要不是由蒸发-凝聚机制引起的气相传质，而是由粉末体内的质点扩散引起的。这类扩散传质主要有体积扩散、表面扩散、晶界扩散和位错扩散等。

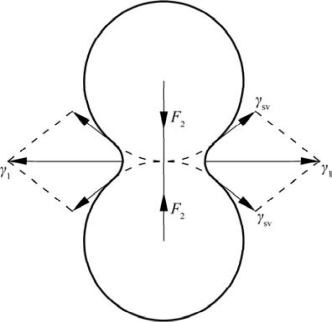
图10.8　粉末双球模型中的应力示意图