总结晶速率将形核和晶体的生长结合起来。人们常用结晶过程中，析出晶体的体积分数和结晶时间的关系来表示总结晶速率。

设一物相α过冷到与它平衡的新相β的稳定区。维持一段时间t后，析出β的体积Vβ，母相α余下的体积为Vα。该相变过程示意如下：

由形核速率Iv的定义，dt时间内形成β的粒子数Nt=VαIvdt。再设β为球形（一个β粒子的体积Vβ），u为β的生长速率（单位时间内球半径的增长），且u与t无关，则在dt时间内，β的体积dVβ可表示为

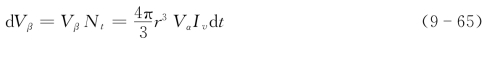
由β的生长速率u的定义，r=ut，将其代入式（9-65）得

在相变初期，晶核间距很大时，相邻晶核间的影响可忽略，并且Vβ很小，Vα=V-Vβ≈V，故式（9-66）可改写为

对上式积分（设Iv、u为常数，给定系统的V是常数）：(www.daowen.com)

式（9-68）即为我们在第6章提到的式（6-4），它适用于相变初期。随着相变的进行，Iv、u开始与时间有关，而且Vα=V-Vβ≠V。因此，1940年前后，Melvin Avrami等对其进行了修正，得到下式：

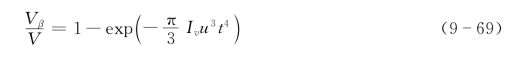
上式称为Johnson-Mehl-Avrami-Kolmogorov或JMAK方程。这种方程最初是由Kolmogorov在1937年得出的。随后，Avrami对此做了研究，并在1939—1941年间发表了一系列论文。因而常称式（9-69）为Avrami方程。后来，I.W.Christion对其做了进一步修正后导出下式：

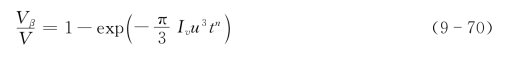
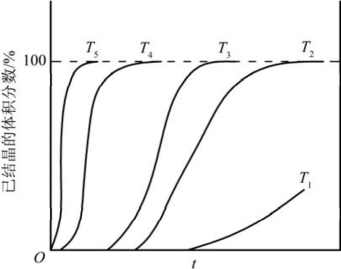
图9.15　不同温度下的结晶体积分数示意图（温度T1＞T2＞T3＞T4＞T5）（引自徐祖耀，1986）

式（9-70）为Avrami方程的一般形式，其中的n为Avrami指数。当Iv随时间t而下降时，n∈［3，4］；当Iv随时间t而增大时，n＞4。式（9-70）描述了新相体积分数随时间t的变化呈s形曲线的变化趋势（图9.15）。

图9.15表明，相变曲线均以Vβ/V=100%的水平线为渐近线。刚开始结晶时，Iv的影响较大，u的影响小，故曲线较平缓。这个阶段主要为下一步的相变创造条件，称为孕育期或诱导期。图9.15还表明温度高，孕育期长。中间阶段由于大量晶核已形成，因而核生长速率u的影响较大，而且是以u3对Vβ/V产生影响，故曲线较陡，Vβ/V迅速增大。相变后期，新相已大量形成，Vβ/V增加较慢，直至接近100%。

在熔液的形核、生长过程中，若尽可能地降低形核速率Iv或者使核的生长受到抑制，则可能会获得玻璃态的物质（请参见6.5.2节）。那么质点是如何在晶核上进行堆砌并产生规则外形的呢？