液滴或气泡内的饱和蒸气压pr与平液面饱和蒸气压p的关系可用Kelvin公式表示：

式中，r为液滴半径；T是温度；其余参数为常数。开尔文公式也可近似地用来描述晶体的溶解度。由于刚开始结晶时的晶核非常小，故假设最初析出的晶核为球形。半径为r的晶核溶解度Er与大晶粒溶解度E的关系为

由上述可见，晶核越小（r越小），晶核的溶解度Er越大。而最初形成的晶核非常小，故晶核的溶解度Er非常大，所以最初形成的晶核会很快溶解。核不能稳定存在，相变也就不能发生。晶核只有足够大，溶解度下降时，它才会在相应条件下稳定存在并长大。那晶核到底要多大才能稳定存在呢？

系统由一相变为两相时，能量有增加，也有下降。系统过冷度ΔT≠0时，系统具有结晶趋势，故结晶会导致系统自由能下降即ΔG1＜0。而新相的形成使系统增加了新的界面（如固液界面），这需要对系统做功，从而导致系统的自由能升高即ΔG2＞0，结果系统的总自由能变化ΔG为

而ΔG1=VΔGV＜0，V为新相体积、ΔGV为单位体积中旧相和新相间的自由能之差G固-G液（以液相结晶为例）。ΔG2=Aγ＞0，其中A为新相的总表面积，γ为新相界面能。此外，原子在新相中重新排列时所占体积与在母相中的体积不同，从而受到阻碍产生应变能ΔG3。应变能阻碍相变进行，故ΔG3＞0。但母相为液体或气体时，ΔG3可忽略。在此，我们只考虑液固相变，忽略应变能。这样，式（9-43）可写为

设晶核为球形，单位体积个数为n，则ΔG可改写成：

用式（9-37）替换ΔGV：

图9.11　晶核大小与Gibbs自由能的关系示意图（引自陆佩文，1991）

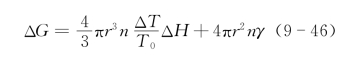
式（9-46）表明相变自由能ΔG是晶核半径r、过冷度ΔT的函数。ΔG与晶核半径r的关系如图9.11所示。

在某一温度下，当晶核半径r较小时，新相界面能ΔG2的增加大于相变自由能ΔG1的减少。这样，系统总的自由能ΔG增加（ΔG＞0），故晶核不能稳定存在而消失。当晶核半径r达到一定程度时（如rk），系统总的自由能ΔG开始发生变化：r＜rk时，晶核半径r越小，系统总的自由能越小，晶核的消失有利于系统的稳定。而r＞rk时，ΔG开始减小。r越大，ΔG越小，直到ΔG＜0。这说明，在晶核半径r＞rk时，晶核越大，越易保存下去。因而，rk被称为临界半径。将式（9-46）对半径r求导：(www.daowen.com)

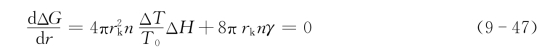
整理得

其中ΔGV=，临界半径rk表示体系自由能ΔG从升高向降低转变时所对应的晶核半径值。

（1）rk越小，晶核越稳定，新相越易形成。设想rk为无穷大，则晶核要想稳定存在并长大，其半径要大于无穷大。显然这是不可能的，即晶核一旦形成就很快消失。相反，若rk为零，只要有晶核形成，其半径肯定大于零，此时的晶核很容易形成并稳定存在。以上两种极端情况，仅用于举例说明rk越小，晶核越稳定，实际并没有这两种极端情形。半径小于rk且不能稳定长大的新相称为核胚（embryo）；半径大于rk且能稳定存在的新相称为晶核（nucleus）。

（2）式（9-48）中，其他参数不变时，过冷度ΔT趋近于零（即温度接近理论相变温度T0），rk趋向于无穷大，这时的系统不发生相变。在式（9-48）中，γ和T0大于零。而结晶是放热过程，ΔH＜0，所以ΔT＞0，即要过冷。ΔT大，晶核rk小，相变容易发生。

（3）用式（9-48）中的rk代替式（9-45）中的r，得到形成rk的晶核时，系统的ΔGk为

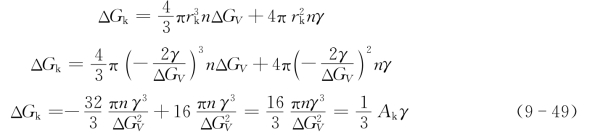
其中Ak=，ΔGk为形核势垒，它表示要形成rk大小的晶核，需要对系统做的功。形核势垒ΔGk的值为新相界面能的1/3。半径r≥rk的晶核摩尔分数可表示为

式（9-50）表明：在单位体积晶核数n不变的情况下，形核势垒ΔGk下降，大于或等于rk的晶核数目nk将增加。

（4）过冷度ΔT与形核势垒ΔGk的关系。将式（9-48）中用到的ΔGV=代入式（9-49）得

由此式可知

式（9-52）表明过冷度ΔT增加，形核势垒ΔGk下降。结合式（9-50），ΔT增加，则系统中大于或等于rk的晶核比例增加，相变容易发生。

晶核的形成主要有两种基本形式——均匀形核和非均匀形核。