这种系统与具有低共熔点的简单二元系统类似。系统处于液态时，组元可以任意比例互溶；在降温过程中，组元的晶相各自从液相中结晶，而且在固态时完全不互溶、不形成固溶体；组元间不发生化学变化。在这种三元立体相图中，三棱柱的每一面都是一个具有低共熔点的简单二元系统，如图8.82（a）所示。这类相图也是分析其他三元相图的基础。因此，我们首先着重介绍这类相图的分析方法。

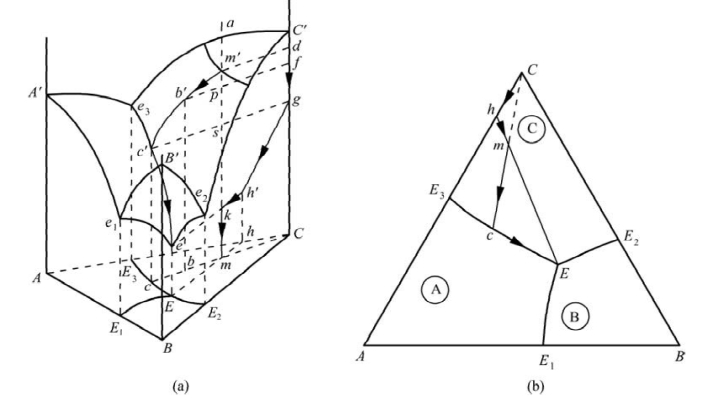
图8.82　简单三元共晶相图

（a）立体图；（b）投影图

图8.82（a）中，e1、e2、e3分别是A-B、B-C、C-A三个二元系统的低共熔点（共晶点），且分别在三棱柱的三个侧面。e为三元系统的低共熔点（共晶点）。这四个共晶点在底面的投影分别是E1、E2、E3、E，如图8.82（b）所示。ee1、ee2、ee3为共晶线，它们是每两个液相面的交界线。这三条共晶线的投影分别为EE1、EE2、EE3。

1.平衡结晶过程

（1）立体图中的过程

我们以立体图中的m组成点为例来说明凝固结晶过程及其获得的组织。把m组成点的系统升温至状态点a（完全熔融）。与二元系统一样，系统在降温、升温过程中，总的系统组成不变，也即m点系统的组成点在降、升温过程中始终在ma线上。ma垂直于底面。

在a点，系统处于液相单相区。系统从a点降温到液相面上的m′点时，由于C晶体在液相面C′e3ee2上达到饱和，故液相在m′点开始析出晶体C（L→C）。此时，固相组成对应在CC′线上的d点。

温度下降时，液相组成仍在C的液相面C′e3ee2上，故从液相中析出的晶体仍只有C。而液相中A、B组元的比例却不会发生变化。根据等比例规则，液相组成在液相面上随温度下降的路线m′c′在底面的投影必为mc，而且cm的延长线必交于C组元的组成点上。在投影图中，液相组成从m向c移动。由杠杆规则，液相在从m′向c′移动的每一时刻，晶相C、液相组成点和系统的总组成点必在一条平行于底面的直线上，如b′pf。这些直线的投影都在mc线上。而系统的总组成点始终都在mm′a线上。因此，平行于底面的直线都在垂直于底面的平面m′b′c′cmCd上。当液相组成点到达c′点时，固相组成到达CC′线上的g点。

因c′在A、C液相面的交界线上，液相在此有共晶反应L—→A+C。A晶相的出现导致固相中含有A、C两个晶相。因此，固相组成点将离开C而在A、C二元系统的面上移动。同时，随着温度下降，液相点沿界线从c′向e点移动，且不断发生共晶反应L—→A+C。液相组成点在从c′向e点移动的过程中，液相、固相组成点和系统总组成点仍是每时每刻都在平行于底面的一条直线上。其中每一条直线与系统总组成点所在直线mm′a构成垂直于底面的平面。温度下降时，这些垂直于底面的平面以mm′a为轴旋转。当液相从c′向e点移动时，固相在A′ACC′面上从g向h′点移动。c′e的投影为cE；A′ACC′面上的gh′线在底面的投影为Ch段。

液相组成到达共晶点e时，四相达成平衡（A、B、C和液相），F=0。共晶反应为L—→A+C+B。由于B晶相的出现，固相组成离开A′ACC′面，而向系统组成线mm′a上的k点移动。在此过程中，温度不变，ekh′为一条平行于底面的直线。当液相消失时，固相到达k点。h′k的投影为hm段，结晶结束。

综上所述，在立体图中，液相组成点的路线为am′c′e；固相路线为dgh′k（如图中箭头所示）。由此可见，立体三元相图的分析比较复杂。但由于三元相图的结晶过程与投影图有对应关系，故人们常常分析三元相图的投影图。

（2）投影状态图中的过程

图8.82中，图8.82（b）为图8.82（a）的投影。投影图有三个大的区域，它们是液相面的投影区。系统组成点在哪个区域，则首先析出的初晶为这个区域的顶点所对应的晶相。图8.82（b）中，AE1EE3为A的初晶区，常用圆圈内标A表示。系统组成点在这个区域内，则首先析出A的初晶。同理，系统组成点在B、C初晶区，则首先析出B、C的初晶。E1E、E2E、E3E为液相面的交界线。液相在这些界线上要发生共晶反应，析出界线两侧的晶相。E点为三元共晶点，在此，液相要同时析出E点周围三个初晶区内的晶相。

对图8.82中的m点系统，它的组成点在C的初晶区内。因此，液相首先析出C晶相。液相从m点开始，固相从C点开始。温度下降，液相从m开始沿Cm的延长线离开m点（满足等比例规则）。在此过程中，C不断从液相中析出，L→C，F=2。(www.daowen.com)

当液相到达界线上的c点时，因c在A、C界线上，故发生共晶反应L—→C+A，F=1。液相组成从c向E移动过程中，因A的出现，固相组成只能在AC线上，且从C向A方向移动。当液相组成到达E点时，固相到达h点。由杠杆规则，液相点、固相点和系统组成点m始终在一条直线上。这好像系统组成点m处有一颗钉子把杆钉住，而形成以m为支点的杠杆。该杠杆的两端分别是液相和固相组成点。液相组成点向温度低的共晶点移动时，杆的另一端固相点也跟着移动。

液相组成在E点发生三元共晶反应，四相平衡L—→A+C+B，F=0。液相在此消失，结晶结束。以上过程，在投影图中的变化路径用下式表示为

液相：

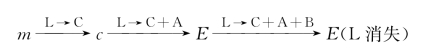
固相：为与液相过程一一对应，我们也列出三个过程：

2.各相量（质量分数、摩尔分数和原子分数）的计算

还是以图8.82中m点系统为例。温度在Td～Tg段时，各相量的计算只能在立体相图中进行。如图8.82（a）所示，当液相到达b′时，液相的质量分数为pf/b′f，固相（只有晶相C）的质量分数为b′p/b′f。液相刚到达c′时，液相的质量分数为sg/c′g，固相（只有晶相C）的质量分数为c′s/c′g。此时及以后的计算，我们可在投影状态图中进行。

当液相刚到达c′时，在图8.82（b）中，液相在c点，其质量分数为mC/Cc，固相的质量分数为mc/Cc。对于液相刚到达c′时，在立体图中的计算值和在投影图中的计算值是相等的，即液相质量分数sg/c′g=mC/Cc、固相质量分数c′s/c′g=mc/Cc。

液相刚到达E点，B还未析出时，液相的质量分数为hm/hE，固相的质量分数为mE/hE。而固相中还含有A、C。此时，固相组成点在h点。由此可知，固相中，A的质量分数为hC/AC。若以AC段为1，则液相刚到达E点时，整个系统中A的质量分数为（mE/hE）hC，C的质量分数为（mE/hE）Ah。

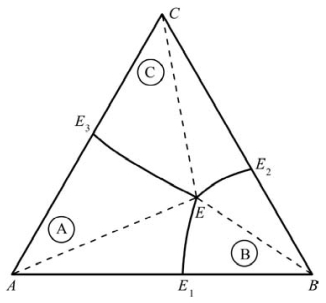
图8.83　投影示意图中的组织区

3.平衡组织

m点的系统在凝固结晶时，首先析出初晶C。在E3E界线上，通过共晶反应，C、A晶相从液相中析出。在E点，A、B、C晶相通过共晶反应而析出。因此，m点的系统在共晶点温度以下的平衡组织为初晶C、共晶C+A及共晶C+A+B。其共晶原理、共晶组织的形貌与二元共晶相似。

我们还可将这类相图分成不同的组织区。图8.83中，我们分别将A、B、C三个组成点与共晶点E相连接，如图中虚线所示。实线围成的三块区域AE1EE3、BE1EE2、CE2EE3分别是A、B、C的初晶区。在同一初晶区内，不同位置的系统组成点，其室温平衡组织有所不同：AE1E区为初晶A、共晶A+B、共晶A+B+C；AE3E区为初晶A、共晶A+C、共晶A+B+C。BE1E、BE2E、CE2E和CE3E区的组织，请读者自行分析。

系统组成点在界线上的不同组织：AE线上为初晶A、共晶A+B+C；E1E线上为共晶A+B、共晶A+B+C。BE、CE、E2E和E3E线上的组织，请读者自行分析。