杠杆规则是分析二元、三元相图的一个重要规则。我们可利用该规则计算系统在一定条件下平衡相间的数量关系。

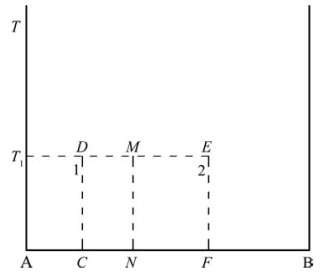
图8.16　杠杆规则的推导示意图

设系统的组成在N点（图8.16）。将该系统升温，如前文所述，因组成不变，系统状态点始终在NM或NM的延长线上。当系统的温度升至T1时，设系统分为两相（如液相和固相），其中1相的状态点在D点，2相的状态点在E点（但整个系统的组成仍是M或N点对应的组成）。设系统的总质量为m，1相的质量为m1、2相的质量为m2，则

对B的质量分数而言，1相中B的质量分数为AC/AB；2相中B的质量分数为AF/AB。就整个系统来说，B的质量分数为AN/AB。根据质量守恒原理，1相和2相中B的质量之和等于整个系统中B的质量，故

式（8-10）和式（8-11）中，消去m，经整理得(www.daowen.com)

由图8.16可知，AN-AC=CN=DM，AF-AN=NF=ME，故式（8-12）可改写为

或写为

式（8-13）与物理学上的杠杆平衡条件“动力×动力臂=阻力×阻力臂”相似，因此式（8-13）和式（8-14）被称为相平衡中的杠杆规则。“支点”为系统组成线上的某点，如T1时，M为支点。

相平衡中的杠杆规则还可表述为当系统处于两相平衡时，可根据系统及两相状态点在相图上的位置，确定平衡两相的数量比。此时，两相平衡共存，两相物质的质量（或物质的量）与两相状态点到系统状态点的距离成反比。也即系统达到相平衡时，某相的状态点离系统状态点越近，则其物质的质量（或物质的量）越大。关于此规则的应用，我们将在后续章节做进一步介绍。下面我们介绍几种常见的二元相图。