1884年，荷兰科学家Jacobus Henricus van't Hoff（1852—1911年）提出了Van't Hoff方程。该方程将化学反应的平衡常数、温度和标准焓变联系起来。在此基础上，瑞典化学家Svante August Arrhenius（1859—1927年）于1889年提出化学反应的速率常数k、温度T和反应活化能的关系式：

此式也可表示为

其中R为摩尔气体常数；A为指前因子。式（7-114）和式（7-115）都被称为Arrhenius方程。

在研究固体中的扩散时，Roberts-Austen猜到了熔化温度对扩散系数起决定性作用。因此，他选择了低熔点的Pb。但人们不清楚Roberts-Austen当时是否认识到了Arrhenius方程表示的扩散动力学与温度的指数关系。到了1922年，Langmuir等已认识到这种关系，即扩散系数D与温度的关系和Arrhenius方程有相似的表达式：

式中D0为指前因子（或频率因子），属于非温度显函数项。跃迁产生的熵变包含在D0中。Ea为扩散活化能。式（7-116）表明温度升高，D增大。这一点可由式（7-113）得到解释。温度升高，扩散体系中处于活化态的原子，其摩尔分数增加，这有利于扩散。比如C在γ-Fe中的扩散，927℃时的扩散系数为1.61×10-11m2/s、1027℃时的扩散系数为4.74×10-11m2/s。根据4.2.3节，我们还知道温度高于0K就会有空位产生。温度升高，空位的摩尔分数增加。晶体中的空位多、原子堆积不紧密，则原子的扩散也容易。因此，受扩散控制的过程，均要考虑温度的影响。

对间隙扩散来说，活化能只包括间隙原子的迁移能。而空位扩散的活化能包括空位形成能和空位迁移能。在实际晶体中，除本征热缺陷外，往往还包括杂质离子固溶所引入的空位。故空位机制的扩散系数应包括晶体中总空位的摩尔分数［V］=［Vin］+［Vex］，［Vin］为本征空位的摩尔分数、［Vex］为杂质空位的摩尔分数。扩散系数与空位摩尔分数的关系包含在指前因子D0中。

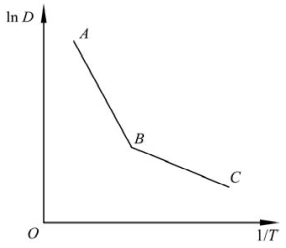
图7.24　扩散系数与温度的关系示意图

将式（7-116）取对数后获得lnD-1/T关系图。但实际上它是一条折线，如图7.24所示。这主要是由本征空位的摩尔分数、杂质空位的摩尔分数谁占优势而引起的。弯折部分发生在本征缺陷的摩尔分数和杂质引起的非本征缺陷摩尔分数相近的温度。温度足够高时（AB段），［Vin］≫［Vex］，扩散由本征空位所控制，此时的扩散为本征扩散；在温度较低时（BC段）［Vin］≪［Vex］，扩散由杂质空位所控制。而且，扩散还受杂质离子的电价、摩尔分数的影响。这种受杂质所控制的扩散称为非本征扩散。NaCl中Na+的扩散系数D与1/T具有这种折线关系。(www.daowen.com)

然而，也有很多物质，其中的扩散也不完全与图7.24所示的情形一致。比如Al2O3、MgO、CaO等的Schottky缺陷生成焓在6eV左右。这些晶体中，杂质的摩尔分数必须小于10-5，我们才能在2000℃左右观察到其中的本征扩散。因此在热缺陷生成焓较大的氧化物中，人们很难观察到本征扩散。这时，lnD-1/T图就不是折线而是一条线段。lnD-1/T图中没有出现折线的另一个原因还可能是测量的温度范围不够大。

还需注意的一点是，晶体中离子的扩散与离子电导有密切关系。离子晶体中的电导主要为离子电导。离子电导有两类：一是本征热缺陷的定向迁移引起的电导——本征电导；二是杂质离子的定向迁移引起的电导——杂质电导。电导率σ与扩散系数D的关系可用下式描述：

式中，n为单位体积内的载流子数；q为一个载流子的荷电量。式（7-117）表明离子的电导率与离子的扩散系数D在一定条件下成正比。将式（7-116）代入式（7-117）：

再由式（4-17）或式（4-24）得

将上式代入式（7-118）得

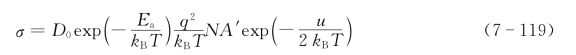
进一步整理可得

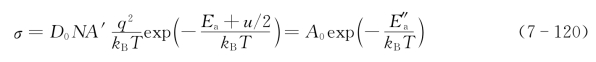
式（7-120）与式（7-116）类似，取对数后也有lnσ-1/T关系图。这是因离子电导与离子的扩散有关，故lnσ-1/T关系图也是一条形如图7.24所示的折线。这是由于杂质离子的扩散活化能比点阵离子的扩散活化能小许多，因此在较低温度下，杂质电导占主导地位（图中BC段）。而在高温下，本征电导或电子电导的作用开始显现。