当原子在各可能位置的跃迁概率相等时，设t秒内，原子经过n次跃迁产生的净位移为Rn。大量原子扩散产生的平均位移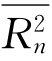可以通过演算（此处忽略）获得：

r的意义同前，它表示一个原子每次的跃迁距离。跃迁频率f表示原子每秒跃迁f次，故在t秒内，原子跃迁的总次数为n=ft。这样原子扩散的平均距离为

将式（7-100）得出的扩散系数D=b2fP中的f代入式（7-108）后，整理得

令=ξ，它是取决于物质结构的几何参数，故

将其开方后得

式（7-111）表明原子扩散位移的均方根与时间的平方根成正比。式（7-110）与式（7-57）是一致的。不过，式（7-110）是从微观原子尺度得到的，而式（7-57）是根据连续介质模型获得的。将式（7-108）与式（7-110）对照后可知：

式（7-112）称为Einstein方程，它将扩散系数D与原子跃迁频率f、跃迁距离r联系起来了。

由Einstein方程，我们也可得出与前文相同的扩散系数表达式。只要由=ξ求出几何参数ξ即可。一维扩散时，r=b，P=1/2，故ξ=2。这样得出的D与式（7-101）得出的D一致。二维情形中，跃迁方向平行于坐标轴，r=b，P=1/4，故ξ=4。简单立方晶体中，r=b=a，P=1/6，故ξ=6。图7.18所示的面心立方晶体中，r=a，P=1/3，故ξ=6。(www.daowen.com)

7.5.1节和7.5.2节从不同角度介绍了D的微观表达式，其实它们是一致的。

例7.4 在恒定源条件下，820℃时，钢经1 h的渗碳，可得到一定厚度的表面渗碳层。若在同样的条件下，要得到两倍厚度的渗碳层需要几个小时？

解：在恒定源及恒温条件下，扩散系数可简化为常数。渗碳可看成是一维方向，则渗碳层厚度x与时间t的关系可运用式（7-57）或式（7-110）、式（7-111）得到

const.表示常数，则

因x2=2x1，故求得t2=4h。

例7.5 在不稳定扩散的条件下，800℃时，在钢中渗碳100 min可得到合适厚度的渗碳层。若在1000℃时，要得到同样厚度的渗碳层，需要多少时间？（扩散系数D800=2.4×10-12m2/s，D1000=3.0×10-11m2/s）。

解：由于涉及扩散系数，故该题运用式（7-110），有

const.′为常数。由于渗碳层厚度相同，所以x1=x2，即

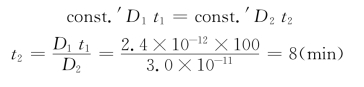
在1000℃时，要得到同样厚度的渗碳层需要8 min。

在学习了扩散驱动力、多元系统中的扩散，以及扩散的微观理论后，我们现在要问的问题是：材料中的原子究竟是怎么扩散的，即扩散机制是什么？