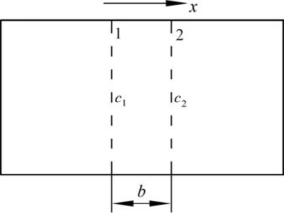
图7.15　晶面间原子的扩散（引自徐祖耀，1986）

设晶体中原子的迁移采取一种类似于Brown运动的无规行走模式（即原子每一步的运动方向与前一步无关）。在此假设下，原子向各方向的跳动概率是一样的、原子的总位移是多次跳动的矢量和。

以一维方向为例（图7.15）。设在x方向的浓度梯度为∂c/∂x。在本节中，我们将浓度c定义为单位体积内的原子个数（单位为个/立方米，这种定义是浓度mol/L的演变）。

在垂直于浓度梯度的方向上有一系列晶面（图7.15中的1、2是其中的两个晶面）。原子在晶面间的迁移遵循无规行走模式，而且相邻晶面间的浓度梯度为无穷小。

再设单位时间内，原子从晶面1跃迁到邻近晶面2的次数（即跃迁频率f）为定值；每个原子在晶面1、2间相互跃迁的概率为P；n1、n2分别为晶面1、2单位面积上的原子数（单位：个/平方米）；晶面1、2的间距为b，b也是原子的跃迁距离。

根据以上假设，单个原子在单位时间内由晶面1跃迁到晶面2的次数为fP；n1个原子在单位时间内由晶面1跃迁到晶面2的次数为n1fP；在dt时间内，n1个原子由晶面1跃迁到晶面2的次数为n1fPdt。同理，在dt时间内，n2个原子由晶面2跃迁到晶面1的次数为n2fPdt。则在dt时间内，从晶面1跃迁到晶面2的净原子数为

由式（7-6），扩散通量可写为

其中N为从晶面1跃迁到晶面2总的净原子数；dN/A表示单位面积内从晶面1跃迁到晶面2的净原子数dn。将式（7-94）代入式（7-95）得

n1还可以表示为c1×b。关于这点，我们代入单位计算就容易明白了：

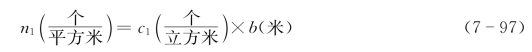
同理，n2也可表示为c2×b。这样式（7-96）就改写为

因为浓度梯度∂c/∂x的物理意义为法线方向上单位距离内的浓度变化。现在，晶面1、2间的间距为b，故这两个晶面间的浓度变化为

将式（7-99）代入式（7-98）得

将式（7-100）与Fick第一定律进行对比，我们可知b2fP即为Fick第一定律中的扩散系数D。因此，D=b2fP可将宏观扩散系数与微观原子的跃迁联系起来。现对D=b2fP做讨论。

（1）一维情况(www.daowen.com)

在一维情况下，某一晶面上的原子可朝x正负方向的两个晶面跃迁，故原子朝其中任一晶面跃迁的概率为P=1/2。跃迁的距离就为x方向的晶面间距b，则

（2）二维情况

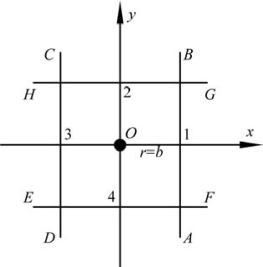
图7.16　二维情形中，原子在晶面间的跃迁示意图（b为晶面间距，r为跃迁距离，1、2、3、4为O点原子可能的跃迁位置）

在二维情况下，原子除了朝垂直于x方向的晶面跃迁外，还可以朝垂直于y方向的晶面产生跃迁。图7.16中，O点处原子可能的跃迁晶面共四个：AB、CD、EF和GH。而每个晶面有一个位置可以提供跃迁。这四个晶面提供的四个位置如图7.16中的1、2、3和4所示，故O点处原子朝其中一个晶面跃迁的概率为P=1/4，则

（3）三维情况

以简单立方晶体为例（图7.17）。在坐标原点的原子可以朝x轴、y轴和z轴正负方向共六个最近邻晶面跃迁。只在一次跃迁的情况下，这些晶面上离跃迁原子太远的位置不可能成为跃迁位置。比如，在图7.17中x的正方向上，O点的原子可以向EFGH面上的E、F、G、H四个位置跃迁，但F、H离O点较E点远，G点更远。因而，EFGH晶面上只有一个E点位置可接纳O点处原子。其他方向的晶面也如此。结果，O点原子周围有六个最近邻晶面。每个最近邻晶面上有一个位置可接纳跃迁来的原子，即O点原子向其中一个晶面的跃迁概率为P=1/6，则

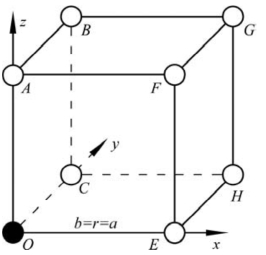
图7.17　简单立方晶体中，原子在晶面间的跃迁示意图

而O点原子从OABC晶面跃迁到EFGH晶面时，跃迁距离r为立方晶体的晶格常数a，即b=r=a，故式（7-103）可改写为

再以面心立方晶体结构（如Cu）中八面体间隙处的原子跃迁为例。图7.18中，八面体间隙处的原子F，其最近邻有12个八面体间隙可供跃迁。我们沿ABCD将晶体剖开，然后投影到xOy面上得到图7.18（b）。

图7.18（a）中，八面体间隙处的原子F所处的晶面为MNST。若F从该晶面朝x轴正方向的HBKC晶面跃迁时，则HBKC晶面上有H、B、K和C四个位置可供跃迁。F原子共有12个最近邻八面体间隙可供跃迁，但从MNST晶面跃迁到HBKC晶面就有四个间隙位可接纳F原子，故F原子从MNST晶面跃迁到HBKC晶面的概率为4/12=1/3，即P=1/3。F原子跃迁到其他晶面的概率也是1/3（这种分析方法同样适用于前面一维、二维情形。只是前面例子中，每个晶面只有一个位置可接纳跃迁原子）。故图7.18中，F原子扩散系数为

其中b为晶面间距。据图7.18（b）所示，b为F原子所在晶面MNST与八面体间隙所在晶面HBKC的间距。该间距为立方晶体晶格常数的一半，b=a/2。将其代入式（7-105）得扩散系数：

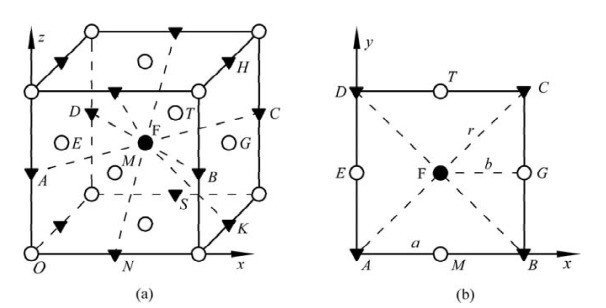
图7.18　面心立方晶体中，八面体间隙中的原子跃迁位置示意图（实心三角形为八面体位置）

式（7-104）和式（7-106）表明：不同晶体结构中的原子，其跃迁路径有所不同。