物理化学和冶金学家Lawrence Stamper Darken（1909—1978年）曾详尽研究了Kirkendall效应。1948年，他发表了其研究结果。他的研究把双组分扩散系统的扩散系数、组元的本征扩散系数和自扩散系数联系起来了。Darken的第一个方程描述了标志物的迁移速率：

该式称为Darken第一方程（Darken's first equation）；其中D1、D2分别为组元1、2在一定浓度梯度下的扩散系数（即分扩散系数或本征扩散系数）；M1、M2分别为组元1、2的摩尔分数；x为距离。在此基础上，Darken利用一维不稳定扩散微分方程、并引入玻耳兹曼变换后获得下式：

该式称为Darken第一方程（Darken's first equation）；其中D1、D2分别为组元1、2在一定浓度梯度下的扩散系数（即分扩散系数或本征扩散系数）；M1、M2分别为组元1、2的摩尔分数；x为距离。在此基础上，Darken利用一维不稳定扩散微分方程、并引入玻耳兹曼变换后获得下式：

其中D为综合扩散系数，即互扩散系数，也是扩散微分方程中的扩散系数，而且实验所测得的扩散系数也是它。利用式（7-84b）、式（7-85b），计算式（7-90），并考虑式（7-85c）的热力学因子相等，得：

其中D为综合扩散系数，即互扩散系数，也是扩散微分方程中的扩散系数，而且实验所测得的扩散系数也是它。利用式（7-84b）、式（7-85b），计算式（7-90），并考虑式（7-85c）的热力学因子相等，得：

式（7-90）和式（7-91）合称为Darken第二方程（Darken's second equation）。式（7-91）将几种扩散系数集合在了一起。Darken方程在1950年芝加哥的那次研讨会上得到了大多数与会者的肯定。对于理想固溶体（γ1=1）、无限稀固溶体（γ1=常数），式（7-91）写为

式（7-90）和式（7-91）合称为Darken第二方程（Darken's second equation）。式（7-91）将几种扩散系数集合在了一起。Darken方程在1950年芝加哥的那次研讨会上得到了大多数与会者的肯定。对于理想固溶体（γ1=1）、无限稀固溶体（γ1=常数），式（7-91）写为(www.daowen.com)

对比式（7-92）等号两边，得

对比式（7-92）等号两边，得

介绍至此，不知读者是否明白了分扩散系数（本征扩散系数）Di、自扩散系数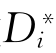、综合扩散系数（互扩散系数）D及Fick定律中的扩散系数D之间的关系。

以上我们从较宏观的角度分析了物质的扩散。但是，我们很少考虑原子的迁移，特别是扩散微分方程是以连续介质方式来处理物质的扩散。而要了解扩散的机理，进而通过控制扩散过程获得一定的材料结构，就需要从原子尺度来理解物质的扩散及其影响因素。

介绍至此，不知读者是否明白了分扩散系数（本征扩散系数）Di、自扩散系数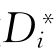、综合扩散系数（互扩散系数）D及Fick定律中的扩散系数D之间的关系。

以上我们从较宏观的角度分析了物质的扩散。但是，我们很少考虑原子的迁移，特别是扩散微分方程是以连续介质方式来处理物质的扩散。而要了解扩散的机理，进而通过控制扩散过程获得一定的材料结构，就需要从原子尺度来理解物质的扩散及其影响因素。