尽管碳在铁管中的wCln r曲线（图7.6）表明扩散系数与浓度c有关，但在求解扩散偏微分方程时，我们经过简化仍认为扩散系数与浓度无关，是一常数。在此基础上，我们获得了一维扩散的微分方程的解析解。上一小节，我们又从热力学方面得出了物质的分扩散系数，其中的热力学因子也表明扩散系数与浓度有关。这样，我们就有一个疑问：是否能由浓度分布求出扩散系数？日本科学家Chuijiro Matano对此做了研究。

1933年，Matano从实验获得的浓度分布曲线出发，计算出了不同浓度时的扩散系数。这种方法称为Matano法。以一维为例，其扩散微分方程为

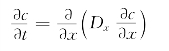
由于Dx与c有关，故不能提到微分符号外面。这样就不能用前面的方法获得其解析解。为此，Matano引入了玻耳兹曼变换。最后，他获得了下式：

因为D与浓度c有关，故在原始界面x=0处的两侧，扩散物质的浓度分布并不对称（图7.11）。若我们假设D是常数，则浓度分布曲线在原始界面x=0的两侧是对称的（图7.8）。为了使某个界面两侧的浓度相等，需做坐标变换x→x′，使得

(www.daowen.com)

引入的这个界面称为俣野面（Boltzmann-Matano interface）。式（7-86）在引入坐标变换后变为

根据式（7-88），由实验可获得在一定温度下，不同浓度时的扩散系数D（c）。

Matano法可以计算D（c）。在此过程中产生的Boltzmann-Matano界面还有一个重要的物理意义：物质经此界面扩散，流入的量与流出的量相等，即图7.11中阴影部分的面积相等。

物质扩散真如Matano界面的物理意义所描述的那样吗？由热力学理论推出的式（7-80）和式（7-81）表明：物质的扩散不一定与Matano界面所描述的情形一样，因为每种物质的扩散系数不一定都相同，但这仍需实验来证实。这个实验主要是由Kirkendall来做的。

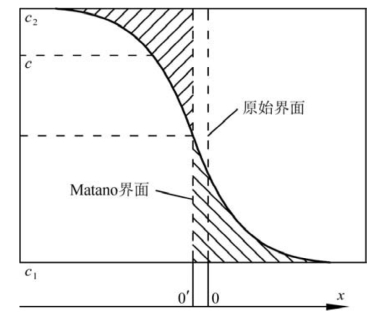
图7.11　Boltzmann-Matano界面示意图（该界面两侧阴影部分的面积相等（引自潘金生，2011）