1.扩散系数的推导

以一维扩散系统为例，设x处的化学势为μx。在x处将该化学势展开成Taylor级数，忽略二阶以上的高阶项，得到x+dx处的化学势：

i原子从x处扩散到x+dx处的驱动力Fi为这两处的化学势梯度∂μ/∂x，表示为

i原子从x处扩散到x+dx处的驱动力Fi为这两处的化学势梯度∂μ/∂x，表示为

梯度的方向由低指向高，扩散方向从高化学势指向低化学势，故式（7-71）中引入负符号。i原子在扩散时，假设其平均速率为vi（cm/s）。vi与Fi呈正比关系，引入常数后写成等式：

梯度的方向由低指向高，扩散方向从高化学势指向低化学势，故式（7-71）中引入负符号。i原子在扩散时，假设其平均速率为vi（cm/s）。vi与Fi呈正比关系，引入常数后写成等式：

其中Bi为迁移率，它表示i在单位驱动力作用下的速率。

由于我们是在原子尺度进行讨论，故本节采用物质的量浓度（也就是常说的浓度）。设i原子的浓度为ci（mol/cm3）。该浓度与速率的乘积：

其中Bi为迁移率，它表示i在单位驱动力作用下的速率。

由于我们是在原子尺度进行讨论，故本节采用物质的量浓度（也就是常说的浓度）。设i原子的浓度为ci（mol/cm3）。该浓度与速率的乘积：

式（7-73）的单位恰好是扩散通量的单位［mol/（cm2·s）］，故i的扩散通量Ji为

式（7-73）的单位恰好是扩散通量的单位［mol/（cm2·s）］，故i的扩散通量Ji为

将式（7-71）和式（7-72）代入式（7-74），得

将式（7-71）和式（7-72）代入式（7-74），得

接下来求式（7-75）中的化学势梯度∂μ/∂x。

接下来求式（7-75）中的化学势梯度∂μ/∂x。

由物理化学知识，i的化学势用浓度表示时可写为+RTlnci，其中是i在标态下的化学势，为常数；R为摩尔气体常数；T为热力学温度。对真实溶液体系，常用活度αi代替浓度αi=γici，其中γi为i的活度系数。因此，i的化学势变为。μi对x求导，可得i的化学势梯度：

由物理化学知识，i的化学势用浓度表示时可写为+RTlnci，其中是i在标态下的化学势，为常数；R为摩尔气体常数；T为热力学温度。对真实溶液体系，常用活度αi代替浓度αi=γici，其中γi为i的活度系数。因此，i的化学势变为。μi对x求导，可得i的化学势梯度：

提出∂ci/∂x：

提出∂ci/∂x：

将式（7-77）代入式（7-75）：

将式（7-77）代入式（7-75）：

整理得

整理得

把上式与Fick第一定律J=-D进行对比，可以发现式（7-79）就是Fick第一定律。但它是根据化学势推导出来的，因此它比J=-D更具普遍性。由式（7-79）可知i的扩散系数为

把上式与Fick第一定律J=-D进行对比，可以发现式（7-79）就是Fick第一定律。但它是根据化学势推导出来的，因此它比J=-D更具普遍性。由式（7-79）可知i的扩散系数为

同理其他原子，如j的扩散系数为

同理其他原子，如j的扩散系数为

其中Di、Dj分别为i原子和j原子在多元扩散系统中的分扩散系数。

对于组元之间无相互作用的理想固溶体或无限稀固溶体，活度系数γi=1或是常数，则式（7-80）变为

其中Di、Dj分别为i原子和j原子在多元扩散系统中的分扩散系数。

对于组元之间无相互作用的理想固溶体或无限稀固溶体，活度系数γi=1或是常数，则式（7-80）变为

式中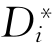为i的自扩散系数。同理，j的自扩散系数为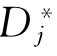=BjRT。若在微观上考虑的话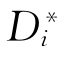也可写为

式中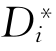为i的自扩散系数。同理，j的自扩散系数为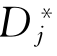=BjRT。若在微观上考虑的话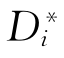也可写为

其中kB为Boltzmann常数。式（7-82）、式（7-83）为能斯特-爱因斯坦方程（Nerst-Einstein equation）。它们表明，在理想固溶体或无限稀固溶体中，不同组元的扩散取决于迁移率的大小。该结论对实际固溶体也适用。式（7-80）和式（7-81）可进一步改写为

其中kB为Boltzmann常数。式（7-82）、式（7-83）为能斯特-爱因斯坦方程（Nerst-Einstein equation）。它们表明，在理想固溶体或无限稀固溶体中，不同组元的扩散取决于迁移率的大小。该结论对实际固溶体也适用。式（7-80）和式（7-81）可进一步改写为

其中 +1为热力学因子。式（7-80）、式（7-81）或式（7-84a）、式（7-84b）表示了物质的分扩散系数与自扩散系数和热力学因子有关。(www.daowen.com)

下坡扩散时，有

其中 +1为热力学因子。式（7-80）、式（7-81）或式（7-84a）、式（7-84b）表示了物质的分扩散系数与自扩散系数和热力学因子有关。

下坡扩散时，有

此时，扩散系数Di＞0，表明物质是从高浓度向低浓度扩散的。

上坡扩散时，有

此时，扩散系数Di＞0，表明物质是从高浓度向低浓度扩散的。

上坡扩散时，有

此时，扩散系数Di＜0，表明物质是从低浓度向高浓度扩散的。

由于i的摩尔分数Mi可写为Mi=ci/∑ci，且对一定的系统而言∑ci是常数。由此，式（7-84a）、式（7-84b）可分别变为

此时，扩散系数Di＜0，表明物质是从低浓度向高浓度扩散的。

由于i的摩尔分数Mi可写为Mi=ci/∑ci，且对一定的系统而言∑ci是常数。由此，式（7-84a）、式（7-84b）可分别变为

在式（7-84a）、式（7-84b）变为式（7-85a）、式（7-85b）的过程中，我们运用了微分理论。因为∑ci是常数，则

在式（7-84a）、式（7-84b）变为式（7-85a）、式（7-85b）的过程中，我们运用了微分理论。因为∑ci是常数，则

其中也称为热力学因子。

2.组元热力学因子之间的关系

恒温、恒压下，均相多组分体系中，各组分的化学势之间存在一定的制约关系，即Gibbs-Duhem方程：

其中也称为热力学因子。

2.组元热力学因子之间的关系

恒温、恒压下，均相多组分体系中，各组分的化学势之间存在一定的制约关系，即Gibbs-Duhem方程：

若多组分体系含有两种组分，则Gibbs-Duhem方程变为

若多组分体系含有两种组分，则Gibbs-Duhem方程变为

现在我们利用摩尔分数Mi=ci/∑ci来表示化学势。将此Mi表达式代入μi=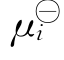+RTln（γici）中，γi与常数∑ci合并后，仍用γi表示，结果得μi=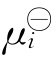+RTln（γiMi）。再将μi表达式代入两组分的Gibbs-Duhem方程M1dμ1+M2dμ2=0中，整理得

现在我们利用摩尔分数Mi=ci/∑ci来表示化学势。将此Mi表达式代入μi=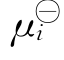+RTln（γici）中，γi与常数∑ci合并后，仍用γi表示，结果得μi=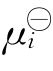+RTln（γiMi）。再将μi表达式代入两组分的Gibbs-Duhem方程M1dμ1+M2dμ2=0中，整理得

因为M1+M2=1，故dM1=-dM2，则

因为M1+M2=1，故dM1=-dM2，则

两边同时除以dM1：

两边同时除以dM1：

因为dM1=-dM2，所以

因为dM1=-dM2，所以

再整理得

再整理得

写成偏微分的形式：

写成偏微分的形式：

结合式（7-84a）、式（7-84b）、式（7-85a）、式（7-85b）和式（7-85c），我们可知：组元i、j的热力学因子相同；组元扩散系数的不同是因迁移率B不同而引起的；扩散系数与浓度c有关。

结合式（7-84a）、式（7-84b）、式（7-85a）、式（7-85b）和式（7-85c），我们可知：组元i、j的热力学因子相同；组元扩散系数的不同是因迁移率B不同而引起的；扩散系数与浓度c有关。