上一节我们介绍了扩散微分方程在几种简单情形下的解。在这些情形中，我们只考虑了一维扩散，而且扩散系数是常数。因此，我们可在适当的边界条件和初始条件下获得这些简单扩散微分方程的准确数值，即解析解。如上文所述，为获得这些微分方程的解析解，我们做了很多简化。而过多的简化会产生误差，甚至错误的结论。此外，扩散系数还是浓度、温度的函数。这时，扩散微分方程是非线性的。通常，我们往往较难获得非线性扩散微分方程的解析解，而较易获得其近似值，即数值解。寻找微分方程数值解的方法称为数值分析方法。目前，求解扩散微分方程的数值分析方法主要是有限元法和有限差分法，其中有限元法应用较广。

如今，人们主要在计算机上采用以上两种方法来求解偏微分方程。这方面，有许多商业软件可供我们使用。比较简单的是Matlab偏微分方程工具箱，较复杂一点的有ANSYS等软件。这两种软件在求解微分方程时主要采用有限元法。利用这些软件，我们可以求解较复杂的二维、三维扩散，也可求解非线性扩散微分方程。当然，如果读者在数值分析方面有一定基础、编程能力强，也可以自己编写有限元或有限差分的程序来求解各种扩散微分方程。利用Matlab偏微分方程工具箱，我们计算了例7.2中的第一种情形，如图7.9所示。该图清楚地展示了在104s时，碳钢中碳的质量分数的分布情况。计算完后，我们不仅可以看到任何时刻的碳的分布情况，还可观看动画，了解碳扩散的动态情况。(www.daowen.com)

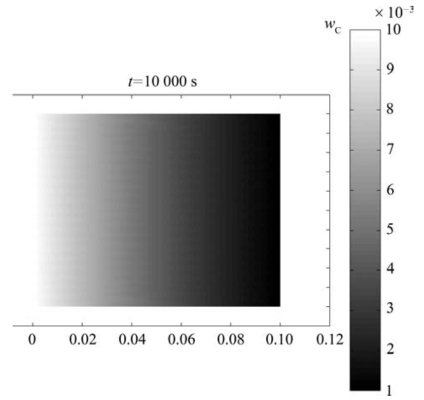
图7.9　Matlab求解例7.2获得的扩散微分方程等值线图（wC为碳的质量分数）