图7.2　扩散微分方程推导所用微元六面体

体系中物质的浓度除了与空间位置有关外，还与时间t有关系。因此，任一点的浓度可表示为c=f（x，y，z，t）。在浓度场中取一六面体微元，如图7.2所示，设其每边边长分别为dx、dy、dz。则微元体积为dV=dxdydz。我们首先考虑物质沿x方向的扩散。假设物质从x处的截面ABCD流入微元，在x+dx处的截面EFGH流出微元。根据流入微元的物质质量-流出微元的物质质量，我们可得到微元中物质的增量。从截面ABCD沿x正方向流入微元的物质质量dmx，可由Fick第一定律得

其中Dx为物质在x方向的扩散系数。

同时，在EFGH处流出微元的物质质量为dmx+dx。dmx+dx可由dmx在x处展开成Taylor级数，并舍去二阶以上的高阶项：

流入微元的物质质量-流出微元的物质质量=dmx-dmx+dx，故有

将式（7-8）代入式（7-10）得

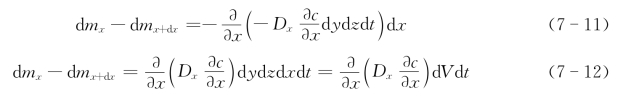
同理，y，z方向的净增量也有类似关系：

因此，微元在dt时间内，物质质量的总净增量dm为式（7-12）、式（7-13）和式（7-14）之和：

(www.daowen.com)

从另一角度来看，设浓度随时间的变化率为∂c/∂t。而质量浓度c是指单位体积的物质质量。所以，在dt时间内，微元dV内物质质量的变化dm′可表示为

因为dm=dm′，故由式（7-15）、式（7-16）建立等式，并整理得

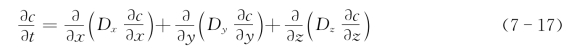
式（7-17）为扩散偏微分方程，也是材料学教科书中通常所称的Fick第二定律（Fick's second law）。若材料各向同性，D与方向无关，则扩散偏微分方程可化简为

式（7-18）也可简写为

其中为Laplace运算符号。当∂c/∂t=0时，浓度不随时间变化，此时属于稳态扩散；当∂c/∂t≠0时，浓度会随时间变化，此时属于非稳态扩散。非稳态扩散有两种情形：∂c/∂t＞0时，浓度会随时间延长而增大；∂c/∂t＜0时，浓度会随时间延长而减小。

现在，我们在一维x方向做分析。x方向的扩散微分方程为

扩散系数Dx＞0。当＞0时，＞0，即浓度会随时间延长而增大。而从数学角度看，二阶偏导＞0表明cx-x曲线在其定义域区间是凹形的。当＜0时，＜0，即浓度会随时间延长而减小。二阶偏导＜0表明cx-x曲线是凸形的。图7.3表示了以上关系。＞0的部分，浓度逐渐增大；＜0的部分，浓度逐渐减小。这种不平衡过程一直持续下去，直至cx-x曲线成一条平行于x轴的直线，从而达到平衡态。

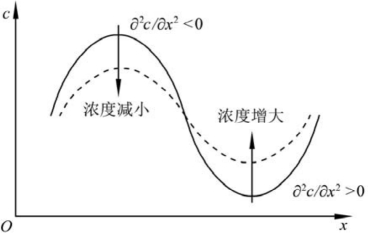
图7.3　一维方向上的扩散微分方程（示意了物质从高浓度向低浓度的扩散）（引自潘金生，2011）

只要我们知道c=f（x，y，z，t）的具体表达式，将其代入式（7-17）或式（7-18）就可获得任何时间、任何位置的浓度分布情况。然而，在实际情况中，我们并不知道，而且也很难获得c=f（x，y，z，t）的表达式。因此，为获得浓度场中各处的浓度分布及变化，我们常常要根据实际情况做一些简化。