1.硬球无规密堆

在第2章，我们已经介绍过Kepler、Hooke和Huygens等曾用球或椭球，Haüy（1743—1822年）用整体分子的堆积来理解晶体的构成，尤其是为什么它们会形成棱、角及平整的面。后来，科学家们把原子当作硬球来处理晶体内部的结构。这些硬球原子的最紧密堆积产生了面心立方和密排六方的晶体结构，堆积系数达到0.74。这是长程有序的规则堆积。如果要产生没有长程序的结构，原子又该做何种形式的堆积呢？

1959年，英国晶体学家John Desmond Bernal（1901—1971年）为阐述液体的结构提出了硬球无规密堆模型（random dense packing model）。为了获得无规密堆，Bernal制作了许多模型来进行研究，如球杆模型、橡皮泥球体的压结、大量滚珠的堆集。他还将钢球装入内壁不平的（避免球有序排列）容器中，然后采用挤压、摇晃等方法使球占有的体积最小，以达到密堆状态。再注入蜡或胶把所有硬球固定，并测量球心的坐标，这样可得到一组无规密堆结构的原子组态。

Bernal提出的硬球无规密堆模型把原子看成等径的硬球。这些硬球如果不接触，相互作用势能为零；硬球一接触则势能为无穷大，即硬球不可被压缩。液体结构由这些硬球无规则地堆积而成。这种堆积使液体的结构均匀、连续而且致密，密度达到最大可能值。模型中没有可以容纳一个硬球的空洞。无规密堆模型能详细描述液体组成粒子的几何平均位置，得到的径向分布函数（RDF）与实验中的真实结构吻合得很好。后来，在研究非晶合金结构时，人们大都以此为出发点，其根本思路从未改变过。

2.无规密堆模型的主要特征

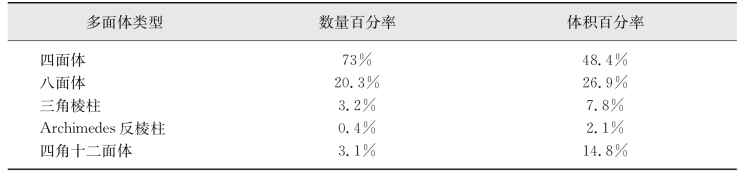
（1）从多面体的堆积来看，无规密堆模型由五种多面体组成，这些多面体简称为Bernal多面体，如图6.9所示。多面体顶点为球心位置，各面是等边三角形。各多面体靠这些三角形连接在一起。在无规密堆模型中，各多面体所占的数量百分率和体积百分率列于表6.1中。在等径球堆积成的面心立方和密排六方晶体结构中，只有正四面体和八面体，而且四面体和八面体的数量比为2∶1。在无规密堆模型中，四面体的数量和体积都大。因此从多面体堆积角度看，四面体是金属玻璃的主要结构单元，它是一种短程局域密堆结构。

图6.9　等径球堆积成的五种Bernal多面体（引自汪卫华，2013）

（a）四面体；（b）正八面体；（c）三角棱柱；（d）Archimedes反棱柱；（e）四角十二面体(www.daowen.com)

表6.1　无规密堆模型中各多面体的数量和体积百分率（引自汪卫华，2013）

（2）只有在三维空间才能做无规密堆，因为二维空间的局域密堆是三角形。而三角形密排的结构是六边形单元，这会导致晶体排列。在三维空间的局域密堆由四面体构成。四面体是具有五次旋转对称的结构单元，不能形成长程序晶体结构。

（3）硬球无规密堆的堆积密度约为0.64，它低于晶体的面心立方密堆和六方密堆的密度值0.74。这表明无规密堆不是真正的密堆，而是一种主要由四面体构成的局域密堆。尽管是一种亚稳排列，但无规密堆在位形空间对应的局域能量极小。无规密堆要转变成晶态密堆需拆散其构形再重新排列，故非晶合金虽然是亚稳态，但还是能长期稳定存在。

根据无规密堆模型我们可通过计算得到金属玻璃的径向分布函数（RDF）、密度和平均最近邻原子数等。这些结构和性质与实际测定的结果基本一致。但是，定量的比较表明这一模型与实验结果还是有些差异，因为无规密堆是等径球堆积的模型，而且不考虑球之间的作用等因素。经过修正，该模型用于金属与类金属组成的非晶合金时（这类合金的结构由两种半径不同的硬球无规密堆而成），计算结果与实测值更加接近。当类金属原子的半径较大、数量较多时，无规密堆模型还是显示其不足的一面。这是由于模型中的间隙尺寸和总间隙体积是有限的。类金属（metalloid）元素主要是指B、Si、Ge、As、Sb、Te等元素。

3.金属玻璃中的无规则网络

金属原子的无规密堆会产生五种Bernal多面体。而早先Zachariasen提出的无规则网络假说就指出玻璃结构是由多面体无规则连接而成的。于是，无规则网络假说也用于理解一些金属玻璃的结构，尤其是金属与类金属组成的玻璃。这种玻璃可以用有一定畸变的三角棱柱体组成的无规网络来描述。其中，金属原子组成三角棱柱体，类金属填充于棱柱体内。这样，原子之间仍然形成紧密堆积。用这种无规则网络模型比用无规密堆模型更能准确地反映类金属元素较多的金属玻璃，如（Ru84Zr16）1-xBx（x=40%～53%）。王文采等用X射线K吸收谱的方法研究了FexGe1-x非晶薄膜的短程结构。他们发现当x＜20%时，FexGe1-x非晶薄膜的短程序结构与非晶Ge的四面体网络十分类似。当x=28.5%时，FexGe1-x非晶薄膜的短程序结构明显偏离非晶Ge的四面体网络，而向配位数增大的密堆结构变化。

在初步了解了玻璃的结构以后，我们再来看看玻璃化转变的实质。