1.Warren对玻璃结构的看法

1927年William Lawrence Bragg来到MIT做了四个月访问学者。其间，Warren被选为Bragg的助手。他们在一起研究了透辉石（diopside）的晶体结构，这是第一个得到研究的链状硅酸盐晶体。两年后，Warren来到英国，在Bragg的实验室学习了一段时间。在那里，他还遇到了Zachariasen。1930年，Warren回到MIT。在没有找到真正的研究兴趣之前，他继续从事硅酸盐晶体结构的研究。但Zachariasen关于玻璃结构的那篇文章发表后，他感到这是一个机会，因为他研究过硅酸盐晶体，对它们的结构比较熟悉。可见，机会是给有准备的人的。并且Debye曾用X射线研究过气体，而其他人用它研究过液体，因而用X射线研究像玻璃一样的非晶体是可行的。于是，Warren开始用X射线研究玻璃结构。事实上，在Warren之前，也有不少人把X射线用于玻璃结构的研究，如前述的John Turton Randall等。但他们都很少去对衍射数据做仔细分析，或者分析的结论不能很好地解释玻璃的一些行为及事实。因此，Warren将其作为研究兴趣进行了多年的研究。结果，他在该领域发表了多篇关于玻璃结构的论文，取得了丰硕的成果。

我们先来看看方石英晶体的基本情况（图3.36做过介绍）。β-方石英（β-cristobalite）是高温稳定型晶体，密度为2.17 g/cm3。α-方石英的密度为2.32 g/cm3。β-方石英与α-方石英在200～270℃之间会发生转变，转变时有明显的体积变化。这个变化是影响晶子假说成立的事实之一。β-方石英为立方晶系，其空间群Fd3m，面心立方点阵，a=b=c=7.16Å，Z=8，原子坐标为Si（0.000，0.000，0.000），O（0.125，0.125，0.125）。β-方石英晶体中Si—O—Si键角为180°。石英玻璃在1000℃以上会转变成β-方石英。

图6.6为石英玻璃和β-方石英晶体在胶片上的X射线衍射花样。图6.6（a）表明石英玻璃在低角度靠近中心的衍射环较宽且模糊。该衍射环对应的衍射角与方石英晶体第一个衍射环的角度几乎一致。方石英第一个衍射环对应其（111）面。方石英的衍射环窄而且清晰，即方石英（111）面对X射线产生了较强的衍射。由于石英玻璃低角度的衍射环与方石英（111）面衍射环几乎一致，晶子假说以此认为玻璃由极细方石英晶体组成。但Warren根据实验数据做了反驳。

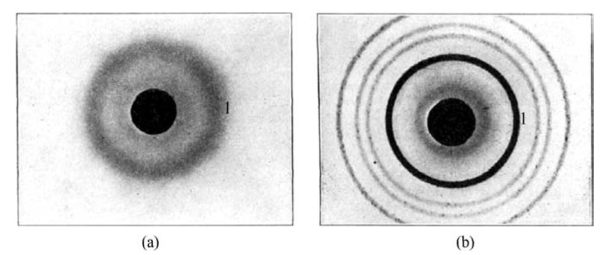
图6.6　X射线衍射花样（两个图中的衍射环1的角度相对应）（引自Warren，1934）

（a）石英玻璃；（b）方石英

从晶胞角度来看，方石英晶体是由其晶胞有规律重复堆砌而成的；从配位多面体角度来看，方石英晶体则是以［SiO4］按一定规律堆砌而成。由于晶体具有周期性和对称性，因此在方石英晶体中，以某一原子为原点，则该原子最近邻原子的数目即配位数是一定的，而且原点处的原子与所有配位原子的距离是一样的。这种情况也适用于次近邻、再次近邻等情形。如图6.7所示，以A处Si原子为原点，其最近邻有四个氧，即Si的配位数为4，形成［SiO4］多面体（图6.7是二维形式）。该Si原子与4个配位数的距离，即键长是相同的。在硅酸盐晶体中，这个平均键长为1.60Å。若以Si—O键长为半径画一个球，则这四个O皆位于球面，即图中第1圈层。次近邻（第2圈层）有4个Si原子，原点处的Si与这4个Si原子的距离也相同。以此类推。若以O原子为原点，也有类似结果。总之，在晶体中，与某一原子相距一定距离之处一定有确定的其他原子，而且这些原子的数目也是确定的。我们知道，晶体有许多在结构上等价或等效的原子。以其中任意一个为原点，在距离原点相同位置的地方，都可找到相同数目和种类的原子。请读者在图6.7中来检查一下是不是这样，其中所有实心球在位置上是等效的，空心球也如此（这也是我们在6.3.2节叙述的位置序）。

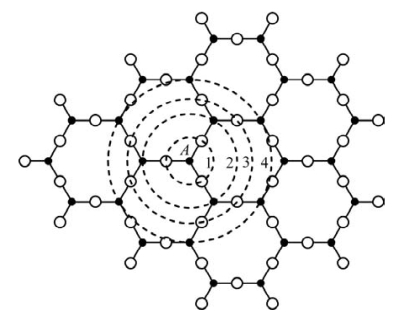
图6.7　二维理想晶体中离选定原子不同距离的原子分布情况示意图

在玻璃结构的研究中，也可采用类似方法考察离开某一原子不同距离处的原子配位情况。Warren根据衍射数据得出石英玻璃中，Si原子与最近邻O原子的距离为1.62Å。这与硅酸盐晶体中Si—O平均键长1.60Å非常接近。他还计算出Si原子的配位数为4.33，这也与［SiO4］中Si的配位数4接近。但随着离选定原子越远（距离大于6.0Å），在不同距离处出现的原子数就取决于［SiO4］的朝向，表现为越来越分散。或者说离选定原子越远，原子随机分布的概率增加，而不像晶体中那么确定。为什么呢？比如，设图6.5（b）为石英玻璃的二维示意图，实心球是Si原子。以任意一个Si为原点，其最近邻有4个O，Si—O键长与硅酸盐晶体中的平均键长接近。但离此原点Si原子越远，键长和其他原子的数目就不像图6.7中所示的那么确定了。不同地方的Si—O—Si键角也有所不同。以任意一个Si为原点，在距离原点相同位置的地方，找到的原子数目也是不同的。这也说明了玻璃中的原子在结构上是不等价的。这种不等价是Zachariasen无规则网络假说的一个内容。以上这种离指定原子一定距离处的原子配位情况常用径向分布函数来表示。请读者查阅资料深入了解。

Warren在做了上述分析后，又重新审视了晶子假说。图6.8展示了衍射强度随衍射角度的变化曲线。它与图6.6是一致的，只是表现方式不同。SiO2玻璃的衍射峰与方石英的低角度第一个特征峰相对应。晶体尺寸小，则晶胞数减少，这会使衍射峰产生持续地展宽。若SiO2玻璃中有足够小的方石英晶体，那么方石英的衍射峰会展宽成SiO2玻璃的衍射峰，这即是晶子假说所坚持的。(www.daowen.com)

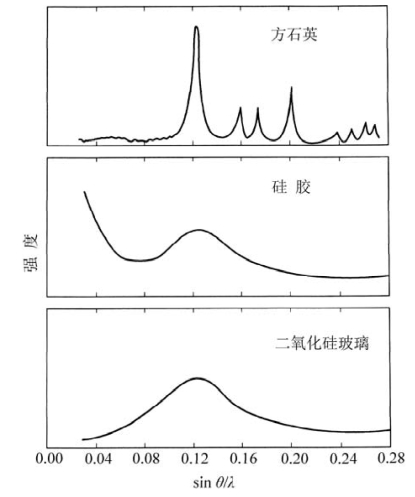
图6.8　方石英、硅胶和二氧化硅的X射线衍射图（引自Warren，1938）

假设SiO2玻璃展宽的衍射峰（或衍射环）是由其中极细的方石英晶体产生的。Warren由此计算出这种极细晶体的尺寸为7.70Å。而β-方石英晶体的晶格常数为7.16Å，这也是β-方石英晶体的晶胞尺寸。由此可见，如果SiO2玻璃中有晶体的话，其尺寸与晶胞尺寸相当。我们在第2章已经学习到，晶体是由晶胞在三维空间有规律重复堆砌而成的。在晶胞尺度上来谈论晶体已使晶体的定义失去了意义。也就是说，叫一个晶胞为晶体，有点勉强。

再一点，玻璃中这些极小的晶体是如何结合在一起的。这些晶体之间有中断吗，或是连续键合在一起而无空缺？玻璃是像鹅卵石装在桶中，还是像水装在桶中？这可由图6.8所示的衍射图来回答。

硅胶的主要衍射峰与玻璃和方石英大约处于同一衍射角。但是，硅胶有非常强的小角度散射，玻璃没有。小角度散射说明硅胶中存在10～100Å大小的不连续颗粒。这些不连续颗粒之间有中断或空缺现象。玻璃与晶体没有小角度散射的现象表明玻璃与晶体一样，其中的键合在本质上是连续的，没有中断和空缺。这也与晶子假说中的“局部不均匀性”相矛盾。

总结一下Warren的结论。在玻璃和方石英晶体中，每个原子的最近邻配位数是一样的。假如我们小到可以坐在其中一个Si原子上，我们只能看到该Si原子的最近邻和次近邻原子，此时的我们不清楚我们是在玻璃还是晶体中。玻璃结构是连续的，键合没有中断和空缺。即使玻璃中有方石英晶体，就晶体尺寸和连接两个分立晶体的非晶层厚度来说，此晶体也只限于极小的区域，而且其尺寸大小不会超过8Å。在这些极小的区域内，玻璃结构是有序的。在较大范围内，玻璃结构并不以晶体的规则形式存在，而是其中的［SiO4］无规则随机堆砌而成，即结构呈远程无序。

Warren等还研究了硅酸盐、GeO2和BeF2玻璃的结构。他们的实验表明，在这些玻璃中，也分别存在［SiO4］、［GeO4］、［BeF4］等配位多面体形成的无规则网络。因此，Warren的实验数据肯定了Zachariasen的无规则网络假说。有了Warren的实验和结论后，玻璃结构是由晶子组成还是无规则网络形成的争论才暂时平息下来。请读者进一步考察一下Warren的实验数据，看看你赞成哪个假说。或者你可以根据这些数据提出一个新的假说。

2.无规则网络假说的改进

无规则网络假说强调了玻璃中原子、多面体相互排列的均匀性、连续性和无序性等。这些结构特征可在玻璃的各向同性、内部性质的均匀性、无固定熔点及性质随成分改变的连续性方面得到反映。因此，在Warren开创性工作后的几十年间，玻璃一直被认为是均质材料。而无规则网络假说则被广泛接受为玻璃结构的最好模型。

随着实验技术的发展和对玻璃结构研究的深入，科学家们发现了玻璃结构中确实存在不均匀现象。当然这种不均匀与晶子假说的不均匀有所不同。采用电子显微镜，科学家们发现在三十到几百埃内，玻璃存在亚微观结构。这种亚微观结构是许多玻璃系统，如硅酸盐玻璃、硼酸盐玻璃等的一个特征。比如，把质量分数为75%（下同）的SiO2、20%的B2O3、5%的Na2O熔融成型为玻璃，再在500～600℃下进行热处理。结果表明玻璃分成了两个不同的相，其中一相几乎是纯SiO2，另一相则富含B2O3和Na2O。这种亚微观结构即为相分离的结果。所谓相分离，简单说就是在高温时液相是均匀的，降温冷却时，液相分成两个或多个液相区（请参阅9.7.3节）。鉴于此，无规则网络假说修正了其观点以接受相分离带来的微不均匀性：玻璃结构存在多种形式的无规则网络。

晶子假说和无规则网络假说主要针对的是当时比较普遍的玻璃，如硅酸盐玻璃。这种玻璃中存在SiO2，而且［SiO4］呈无规则连接。根据3.12.6节的介绍，我们可知：在这种结构中，原子间的共价键作用导致原子的堆积不是最紧密的。这种非最紧密堆积在共价晶体及其玻璃中都存在。金属玻璃出现以后，无规则网络假说就不怎么适用了，因为金属原子间大多以金属键结合在一起。金属键无方向性和饱和性，因此，为使系统能量达到最低，金属原子往往要堆积到尽可能紧密的程度。这就需要新的模型来说明金属玻璃微观结构与性能的关系。