前述表面能主要针对固体与气体、固体与真空的界面——表面而言的。在材料领域还经常遇到固体与固体（如晶界）、固体与液体的接触界面。在上一章，我们对晶界结构及晶界能做了介绍。其他固-固界面与晶界有相似的结构与界面能模型及理论。

多晶材料的晶界在形成后，并不是一成不变的。材料在加工制备（如金属的热处理、陶瓷的烧结）等过程中，其晶界会发生迁移而改变形状。而且，界面的结构和能量还决定了合金中第二相组织的平衡形貌，也即界面能量对界面构型、显微结构有影响。

1.固-固界面

假设一个具有任意曲率半径的大角度界面，其界面能γ为常数。根据式（5-8），系统自由能要下降，则需要减小面积，故界面有平直化的趋势以降低界面面积。在二维平面上看，表示界面的线条有倾向于直线的趋势。

设有三个晶粒相交于三叉晶界。图5.15为该三叉晶界的二维截面图。三个晶界的界面能设分别为γ1、γ2、γ3。在点O，我们取一垂直于纸面的单位长度，则总的界面能为

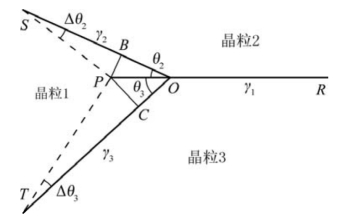
图5.15　三叉晶界平衡条件分析示意图（引自潘金生，2011）

令点O移动微小距离至点P。晶粒1和3、1和2间的晶界将发生转动，晶界位置发生改变。改变后，总的界面能还包括扭转项：

当界面能差为零时，过程达到平衡：

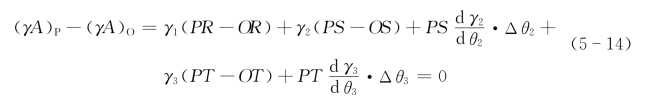
因为OP为无穷小，且PB⊥OS、PC⊥OT，故

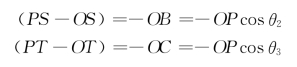
在△BPS中，PB=PS·sinΔθ2，Δθ2很小，故PB≈PS·Δθ2。而在△OPB中，PB=OPsinθ2，所以

同理在△PTC和△OPC中，也有

将以上四个式子代入式（5-14）得

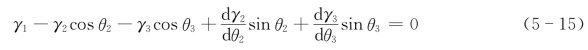
如果γ各向同性，γ1=γ2=γ3，界面能不随取向变化，则式（5-15）后两项为0。令θ2=θ3=θ，则式（5-15）变为(www.daowen.com)

解上式得θ=60°，即晶粒界面的平衡形态与界面投影相互成120°。在二维平面上，晶粒为六边形可满足此要求。小于六边形的晶粒具有外凸晶界，而大于六边形的晶粒具有内凹晶界。这样才能尽可能保持界面间的120°角，即在界面交点处，两条界面的切线夹角尽可能保持120°（图5.16）。在界面曲率的作用下，小于六边形的晶粒缩小，大于六边形的晶粒长大。

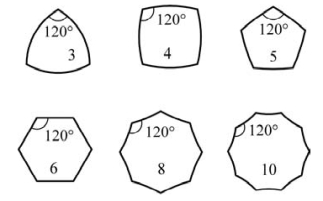
图5.16　平衡晶粒的边界示意图（引自潘金生，2011）

由于四个晶粒相遇形成的晶界会分解成三叉晶界，使系统界面能降低，故实际显微组织中极少观察到四叉晶界。

2.固-液界面

图5.17　固-固-液平衡的二面角（引自Kingery，2010）

如果在两个固相界面处存在一定的液相（图5.17），则界面张力达到平衡时有以下关系式：

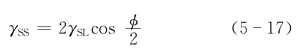
式中，γSS为两固相界面的界面张力；γSL为固液界面的界面张力；φ为二面角。若把液体换成气体，则φ称为热腐蚀角或槽角。式（5-17）还可变换为下式：

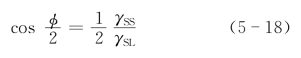
当γSS/γSL≥2时，cos≥1，=0°，则φ=0°。此种情况下，液相在晶界上达到润湿的最高层次——铺展。液相穿过晶界而达到平衡时，各晶粒完全被液相隔开，如图5.18（a）所示。

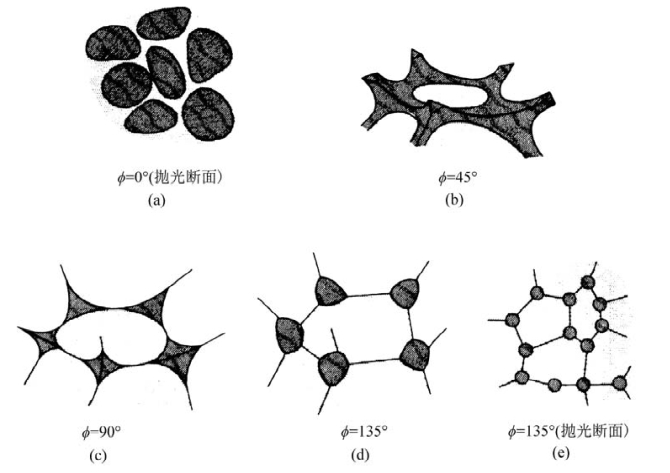
图5.18　不同二面角情况下的第二相分布（引自Kingery，2010）

当＜30°，则φ＜60°。此时，液相能浸湿晶粒，并稳定地沿各晶界渗入，而在三相交界处形成三角棱柱体，如图5.18（b）所示。

当，则60°＜φ＜120°。此时，液相对晶界的润湿性下降，故部分液相渗入固固晶界，如图5.18（c）所示。

当γSS/γSL＜1时，即固-固晶界能小于固-液界面能。cos，则φ＞120°。此时，液相不能浸湿只能粘湿晶粒而在晶界处形成孤立液滴，如图5.18（d）、（e）所示。以上情况常常出现在陶瓷和粉末冶金的液相烧结过程中。

如果把上述液相换成是另一种固相，如在晶界、晶棱等位置析出的第二相。当这些第二相引起的应变能不大时，则其平衡形貌与界面能的相对大小有关系。设固态基体相间的界面能为γαα，第二相与基体间的界面能为γαβ。γαα/γαβ的大小对第二相在晶界处平衡形貌的影响与图5.18所示情形相类似。这种情形在金属材料中比较常见。

固-液界面上第二相的分布涉及润湿的三个层次。若在材料制备过程中有液相的参与，则液相是否能润湿固体对材料界面的结合就显得很重要。比如，陶瓷与金属的封接、金属陶瓷中金属是否与陶瓷颗粒结合紧密等都与润湿有关。