1.表面二维格子

表面原子通过重建可在表面形成有序结构。吸附或沉积外来原子也可能在表面形成有序结构。研究表面原子（含吸附、沉积原子和分子）的排列规律是表面物理的内容之一。

在第2章中，我们介绍了从三维晶体中抽象出的14种布拉维格子；晶胞是能充分反映晶体结构特征（周期性、对称性）的最小构造单位。描述晶胞是用x、y、z晶轴上的单位矢量，即基矢a、b、c来表示的。与三维晶体中布拉维格子、晶胞和基矢的选取相类似，在二维表面的有序结构中，人们也抽象出相应的格子、“晶胞”和基矢。表面上的“晶胞”也是最小重复单元，称为原格（unit mesh）。这与三维晶体的晶胞（unit cell）相对应。原格也要反映表面有序结构的周期性和对称性。理论上已经证明，二维布拉维格子只有五种（图5.4）和四个晶系（表5.1）。

表5.1　表面结构的四个晶系（P为原始，C为带心）（引自曹立礼，2007）

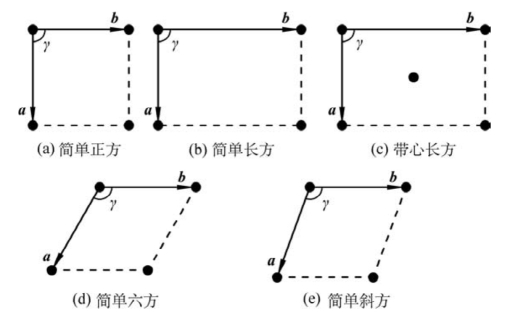
图5.4　表面布拉维格子（引自Bechstedt，2007）

2.表面二维结构表示

描述表面二维重建结构的方法主要有两种，一种是Wood符号标记，另一种是矩阵表示。本书只介绍Wood符号。

最简单的情况是重建层的原格基矢与未重建体相基底的基矢相互平行。而且，原格基矢和基底基矢的模呈简单整数比关系，即：

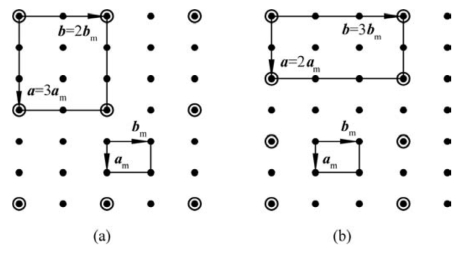
式中，a、b为表面二维原格基矢；am、bm为基底基矢；p、q为简单整数。据此，重建表面可写成（p×q）的形式。如图5.5（a）所示，重建后的二维原格基矢为a=3am，b=2bm。结合式（5-1），可得p=3，q=2，故图5.5（a）形成了（3×2）形式的重建。同理，图5.5（b）的表面重建形式为（2×3）。

(www.daowen.com)

图5.5　表面重建示例1（a、b为表面二维原格基矢，am、bm为未重建基底的原格基矢。为使图清晰，用实心球表示基底格点，空心球表示重建后的格点，但并不是说重建格点要大于基底格点）（引自曹立礼，2007）

然而，在表示表面二维重建原格基矢时，我们还需考虑哪种晶体在哪个表面产生了重建。结合这几个因素，以上这种简单的表面二维原格，其基矢符号为

其中S为基底晶体，（hkl）为重建晶面。比如，晶面劈开或解理后，表面产生重建的有Si（111）-（7×7）、Ni（100）-（2×2）、Rh（110）-（2×2）等。其中，Si（111）-（7×7）最负盛名，也最有代表性，是半导体重构的代表。Si（111）-（7×7）于1959年被发现，其表面结构的相变对半导体表面在原子水平上的物理化学特性的认识有重要意义，从而吸引了很多人对其进行研究。

除了以上简单的表面重建符号外，还有一般的情形，即表面二维重建基矢为基底基矢的线性组合。其二维原格基矢符号为

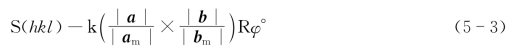
其中k为表面格子的原格符号（表5.1），原始格子可以省略符号P。Rφ°表示重建基矢相对于基底基矢的旋转角度（有时可省略R）即a与am的夹角。如果此角度为0°，则回到上面最简单的情形，通常忽略不写。其余符号同前，如图5.6（a）所示。在图5.6（b）中，虚线所表示的重建基矢是带心的（2×2），可以表示为S（hkl）-C（2×2）。此种带心格子还有一种选法，就是相对于基底基矢旋转一定角度，如图5.6（b）中实线表示的格子，其基矢a、b。假设图5.6（b）中|am|=|bm|，基矢a相对于am旋转了45°，则重建格子表示为S（hkl）-R45°。这类一般的情形如α-Al2O3的重建Al2O3（0001）-R±9°。

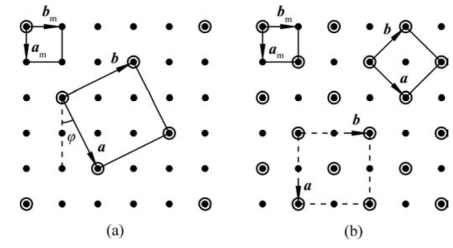
图5.6　表面重建示例2（实心球和空心球的意义同图5.5）（引自曹立礼，2007）

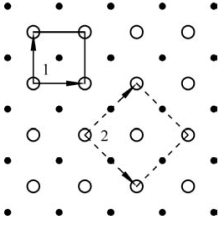
图5.7　TiC（001）面的（1×1）和C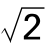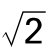（×）“重建”（实心、空心球分别为C、Ti原子）

我们也可以把弛豫产生的表面结构看成是特殊形式的表面重建。此时“重建”的基矢与基底基矢方向、大小都一样。以TiC为例。TiC（001）面原子只作平行于表面法线的弛豫，沿垂直于表面法线方向没有位移。图5.7为TiC（001）面的俯视图。选择图5.7中1所示的原格时，其Wood符号为TiC（001）-（1×1）。但有时在理论研究中，这种原格满足不了需求。于是，我们取大一点的格子，如图5.7中2所示的格子。格子2的矢量相对于格子1旋转了45°，其Wood符号为TiC（001）-CR45°。因此，表面二维格子及其Wood符号不仅适用于表面重建，也可用于表面弛豫，还可以表示表面吸附和沉积产生的有序结构。有关吸附产生的有序结构，我们在实际表面结构中做介绍。